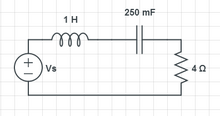
series LRC circuit ... find voltage across the resistor Given that the source voltage is (2t-3t2 ), find voltage across the resistor.
This is the VL solution.
Outline:
H
(
s
)
=
V
L
V
S
=
s
4
+
s
+
1
0.25
s
{\displaystyle H(s)={\frac {V_{L}}{V_{S}}}={\frac {s}{4+s+{\frac {1}{0.25s}}}}}
simplify(s/(4 + s + 1/(0.25*s)))
H
(
s
)
=
s
2
s
2
+
4
s
+
4
{\displaystyle H(s)={\frac {s^{2}}{s^{2}+4s+4}}}
solve(s^2 + 4.0*s + 4.0,s)
There are two equal roots at s = -2, so the solution has the form:
V
L
h
(
t
)
=
A
e
−
2
t
+
B
t
e
−
2
t
+
C
1
{\displaystyle V_{L_{h}}(t)=Ae^{-2t}+Bte^{-2t}+C_{1}}
After a long time attached to a unit step function source, the inductor has shorted and the capacitor has opened. All the drop is across the capacitor.
V
L
p
=
0
{\displaystyle V_{L_{p}}=0}
This also means that C1 has to be zero.
So far the full equation is:
V
L
(
t
)
=
A
e
−
2
t
+
B
t
e
−
2
t
{\displaystyle V_{L}(t)=Ae^{-2t}+Bte^{-2t}}
Initial voltage is all across the inductor.
V
L
(
0
)
=
1
=
A
{\displaystyle V_{L}(0)=1=A}
A
=
1
{\displaystyle A=1}
At this point will have to do integral .. to get to the current. There is no other way to use the known initial conditions: current (initially zero), and VC (initially zero). Will have to introduce integration constant and then evaluate that. More chance of mistakes, more complex, so start over with something else.
i
(
t
)
=
1
L
∫
0
t
V
L
(
t
)
d
t
=
∫
0
t
(
e
−
2
x
−
B
(
x
)
e
−
2
x
)
d
x
{\displaystyle i(t)={\frac {1}{L}}\int _{0}^{t}V_{L}(t)dt=\int _{0}^{t}(e^{-2x}-B(x)e^{-2x})dx}
f := (exp(-2*x) - B*x*exp(-2*x));
S :=int(f,x=0..t)
i
(
t
)
=
B
∗
(
e
−
2
t
(
2
t
+
1
)
4
−
1
4
)
−
e
−
2
t
2
+
1
2
+
C
1
{\displaystyle i(t)=B*({\frac {e^{-2t}(2t+1)}{4}}-{\frac {1}{4}})-{\frac {e^{-2t}}{2}}+{\frac {1}{2}}+C_{1}}
i
(
0
)
=
0
=
C
1
{\displaystyle i(0)=0=C_{1}}
Ok so C1 is zero. Now need to find B.
Find B by doing another integral to get VC :
V
C
(
t
)
=
1
C
∫
0
t
i
(
t
)
d
t
=
4
∗
∫
0
t
(
B
∗
(
e
−
2
t
(
2
t
+
1
)
4
−
1
4
)
−
e
−
2
t
2
+
1
2
)
d
x
{\displaystyle V_{C}(t)={\frac {1}{C}}\int _{0}^{t}i(t)dt=4*\int _{0}^{t}(B*({\frac {e^{-2t}(2t+1)}{4}}-{\frac {1}{4}})-{\frac {e^{-2t}}{2}}+{\frac {1}{2}})dx}
f := (4*(B*(exp(-2*x)*(2*x+1)/4 -1/4) - exp(-2*x)/2 + 1/2));
S :=int(f,x=0..t)
V
C
(
t
)
=
B
+
2
t
+
e
−
2
t
−
B
t
−
B
e
−
2
t
−
B
t
e
−
2
t
−
1
+
C
1
{\displaystyle V_{C}(t)=B+2t+e^{-2t}-Bt-Be^{-2t}-Bte^{-2t}-1+C_{1}}
V
C
(
0
)
=
0
=
B
+
1
−
B
−
1
+
C
1
{\displaystyle V_{C}(0)=0=B+1-B-1+C_{1}}
C
1
=
0
{\displaystyle C_{1}=0}
Still doesn't help us find B. Guess B = 2 since (2t-Bt) has to equal zero if VC is going to converge on 1. Then see if VC (∞) = 1:
V
C
(
t
)
=
2
+
e
−
2
t
−
2
e
−
2
t
−
2
t
e
−
2
t
−
1
{\displaystyle V_{C}(t)=2+e^{-2t}-2e^{-2t}-2te^{-2t}-1}
At t = ∞ what is the 2te-2t term's value?
limit(B*t*exp(-t),t = infinity)
Mupad says 0.
V
C
(
∞
)
=
2
−
1
=
1
{\displaystyle V_{C}(\infty )=2-1=1}
Yes! B = 2 works ... looks like the only thing that works .... So:
i
(
t
)
=
2
∗
(
e
−
2
t
(
2
t
+
1
)
4
−
1
4
)
−
e
−
2
t
2
+
1
2
=
t
e
−
2
t
{\displaystyle i(t)=2*({\frac {e^{-2t}(2t+1)}{4}}-{\frac {1}{4}})-{\frac {e^{-2t}}{2}}+{\frac {1}{2}}=te^{-2t}}
simplify(2*(exp(-2*t)(2*t+1)/4-1/4) - exp(-2*t)/2 + 1/2)
This means that VR is:
V
R
(
t
)
=
4
∗
i
(
t
)
=
4
t
e
−
2
t
{\displaystyle V_{R}(t)=4*i(t)=4te^{-2t}}
Taking the derivative of the above get:
V
R
δ
(
t
)
=
4
e
−
2
t
−
8
t
e
−
2
t
{\displaystyle V_{R}\delta (t)=4e^{-2t}-8te^{-2t}}
V
R
(
t
)
=
∫
0
t
(
4
e
−
2
(
t
−
x
)
−
8
(
t
−
x
)
e
−
2
(
t
−
x
)
)
(
2
x
−
3
x
2
)
d
x
{\displaystyle V_{R}(t)=\int _{0}^{t}(4e^{-2(t-x)}-8(t-x)e^{-2(t-x)})(2x-3x^{2})dx}
f := (4*exp(-2*(t-x)) - 8*(t-x)exp(-2*(t-x)))*(2*x-3*x^2);
S :=int(f,x=0..t)
V
R
(
t
)
=
8
−
8
e
−
2
t
−
10
t
e
−
2
t
−
6
t
{\displaystyle V_{R}(t)=8-8e^{-2t}-10te^{-2t}-6t}
There will not be any constant since again, V_R(t) = 0 after a long time ... and the capacitor opens.