Circuit Theory/1Source Excitement
Jump to navigation
Jump to search
Phasors:
- Called the "Steady State Solution" solution
- Sometimes the "Steady State Solution" resulted in a complete solution, sometimes a partial solution.
- Full "Steady State Solutions" involved integrals and derivatives
- Partial "Steady State Solutions" involved non-homogeneous ODE differential equations
- The partial "Steady State Solution" is called the "Particular solution".
- The Laplace Solution is a complete solution that is identical to Phasor/Complex Frequency when eliminating operators in a differential equation (s or jω), but translates the driving function (current or voltage source) into the Laplace domain differently. The Laplace Solution can translate any driving function. Phasors can only translate sinusoidals. The Convolution Integral (coming up) is easier than either.
Now we are going to finish solving the some of the incomplete, particular "Steady State Solutions."
- The non-homogeneous ODE equation is turned homogeneous by setting the driving function (voltage or current source) to zero and then using either the "Method of undetermined coefficients" or "Variation of parameters" to find the overall solution. The method illustrated here is the "Method of undetermined coefficients".
- This is called the "Transient" or Homogeneous Solution.
- The Homogeneous Solution is found in the time domain, not phasor domain
- Reduce circuit to thevenin or norton equivalent and solve for a single component (or group or components)
- Add Particular + Homogeneous Solution, then evaluate constants.
Click on the numeric solutions to see where they came from. Clicking on particular solutions or non-diff-eq solutions will bounce back to phasor examples.
| Calculus | diff eq | LR | LR Solution | Similar RC |
|---|---|---|---|---|
 |
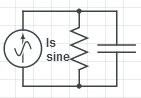 | |||
 |
already solved ... no differential equation! |
 | ||
 |
already solved ... no differential equation! |
 | ||
 |
 |












