Cellular Automata/Neighborhood

1D neighborhood

Since in 1D there are no shapes, the definition of the neighborhood is usually very simple.

Radial neighborhood

Radial neighborhood

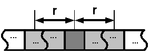
Usually the neighborhood in 1D is described by its radius r, meaning the number of cell left and right from the central cell that are used for the neighborhood. The output cell is positioned at the center.

Formal definition

Formally the radial neighborhood is the set of neighbors

$N = \{-r,-(r-1),\dots,-1,0,1,\dots,r-1,r\}$

or simply the neighborhood size k = 2r + 1 with the output cell at the center k₀ = r.

Symmetries

• reflection symmetry

Stephen Wolfram's notation

In Wolframs's texts and many others the number of available cell states | S | and the radius r are combined into a pair

$(|S|,r) \,$

See also

• Stephen Wolfram, Statistical Mechanics of Cellular Automata (1983)

Brickwall neighborhood

Brickwall neighborhood

An unaligned neighborhood, usually the smallest possible k = 2. The output cell is positioned at k₀ = 0.5 between the two cells of the neighborhood. It is usually processed by alternatively shifting the output cell between k₀ = 0 and k₀ = 1.

2D neighborhood

von Neumann neighborhood

von Neumann neighborhood

It is the smallest symmetric 2D aligned neighborhood usually described by directions on the compass N = {N,W,C,E,S} sometimes the central cell is omitted.

Formal definition

Formally the von Neumann neighborhood is the set of neighbors

N = {{0, − 1},{ − 1,0},{0,0},{ + 1,0},{0, + 1}}

or a subset of the rectangular neighborhood size k_x = k_y = 3 with the output cell at the center k₀x = k₀y = 1.

Symmetries

• reflection symmetry
• rotation symmetry 4-fold

See also

• [mathworld] - [von Neumann Neighborhood]

Moore neighborhood

Moore neighborhood

Is a simple square (usually 3×3 cells) with the output cell in the center. Usually cells in the neighborhood are described by directions on the compass N = {NW,N,NE,W,C,E,SW,S,SE} sometimes the central cell is omitted.

Formal definition

Formally the Moore neighborhood is the set of neighbors

N = {{ − 1, − 1},{0, − 1},{1, − 1},{ − 1,0},{0,0},{ + 1,0},{ − 1, + 1},{0, + 1},{1, + 1}}

or simply a square size k_x = k_y = 3 with the output cell at the center k₀x = k₀y = 1.

Symmetries

• reflection symmetry
• rotation symmetry 4-fold

See also

• [mathworld] - [Moore Neighborhood]

Margolus neighborhood

reversible

see also [1]

Unaligned rectangular neighborhood

Unaligned rectangular neighborhood

An unaligned (brickwall) rectangular neighborhood, usually the smallest possible k_x = k_y = 2. The output cell is positioned at k_0x = k_0y = 0.5 between the four cells of the neighborhood. It is usually processed by alternatively shifting the output cell to k_0x = k_0y = 0 and k_0x = k_0y = 1.

Hexagonal neighborhood

Hexagonal neighborhood

Hexagonal neighborhood

Symmetries

• reflection symmetry
• rotation symmetry 6-fold

Small unaligned hexagonal neighborhood

Unaligned hexagonal neighborhood

Formal definition

Formally the small (3-cell) unaligned hexagonal neighborhood represented on a rectangular lattice is the set of neighbors

N = {{0,0},{1,0},{0,1}}

Symmetries

• reflection symmetry
• rotation symmetry 3-fold

References

• [mathworld] - [Neighborhood]