1. Find parametric equations describing the line segment from P(0,0) to Q(7,17).
x=7t and y=17t, where 0 ≤ t ≤ 1
x=7t and y=17t, where 0 ≤ t ≤ 1
2. Find parametric equations describing the line segment from

to

.


3. Find parametric equations describing the ellipse centered at the origin with major axis of length 6 along the x-axis and the minor axis of length 3 along the y-axis, generated clockwise.


Sketch the following polar curves without using a computer.
22.

23.

24.

Sketch the following sets of points.
25.

26.

Calculus in Polar Coordinates[edit | edit source]
Find points where the following curves have vertical or horizontal tangents.
40.

Horizontal tangents occur at points where  . This condition is equivalent to
. This condition is equivalent to 
 .
.
Vertical tangents occur at points where  . This condition is equivalent to
. This condition is equivalent to 
 .
.

The condition for a horizontal tangent gives: 




Horizontal tangents occur at  which correspond to the Cartesian points
which correspond to the Cartesian points  and
and  .
.
The condition for a vertical tangent gives: 




Vertical tangents occur at  which correspond to the Cartesian points
which correspond to the Cartesian points  and
and  .
.
Horizontal tangents at (2,2) and (2,-2); vertical tangents at (0,0) and (4,0)
Horizontal tangents occur at points where  . This condition is equivalent to
. This condition is equivalent to 
 .
.
Vertical tangents occur at points where  . This condition is equivalent to
. This condition is equivalent to 
 .
.

The condition for a horizontal tangent gives: 




Horizontal tangents occur at  which correspond to the Cartesian points
which correspond to the Cartesian points  and
and  .
.
The condition for a vertical tangent gives: 




Vertical tangents occur at  which correspond to the Cartesian points
which correspond to the Cartesian points  and
and  .
.
Horizontal tangents at (2,2) and (2,-2); vertical tangents at (0,0) and (4,0) 41.

Horizontal tangents occur at points where  . This condition is equivalent to
. This condition is equivalent to 
 .
.
Vertical tangents occur at points where  . This condition is equivalent to
. This condition is equivalent to 
 .
.

The condition for a horizontal tangent gives: 




Horizontal tangents occur at  which correspond to the Cartesian points
which correspond to the Cartesian points  ,
,  ,
,  , and
, and  . Point
. Point  corresponds to a vertical cusp however and should be excluded leaving
corresponds to a vertical cusp however and should be excluded leaving  ,
,  , and
, and  .
.
The condition for a vertical tangent gives: 







Vertical tangents occur at  which correspond to the Cartesian points
which correspond to the Cartesian points  ,
,  , and
, and  .
.
Horizontal tangents at (r,θ) = (4,π/2), (1,7π/6) and (1,-π/6); vertical tangents at (r,θ) = (3,π/6), (3,5π/6), and (0,3π/2) Horizontal tangents occur at points where  . This condition is equivalent to
. This condition is equivalent to 
 .
.
Vertical tangents occur at points where  . This condition is equivalent to
. This condition is equivalent to 
 .
.

The condition for a horizontal tangent gives: 




Horizontal tangents occur at  which correspond to the Cartesian points
which correspond to the Cartesian points  ,
,  ,
,  , and
, and  . Point
. Point  corresponds to a vertical cusp however and should be excluded leaving
corresponds to a vertical cusp however and should be excluded leaving  ,
,  , and
, and  .
.
The condition for a vertical tangent gives: 







Vertical tangents occur at  which correspond to the Cartesian points
which correspond to the Cartesian points  ,
,  , and
, and  .
.
Horizontal tangents at (r,θ) = (4,π/2), (1,7π/6) and (1,-π/6); vertical tangents at (r,θ) = (3,π/6), (3,5π/6), and (0,3π/2) Sketch the region and find its area.
43. The region inside the petals of the rose

and outside the circle

60. Find an equation of the sphere with center (1,2,0) passing through the point (3,4,5)
The general equation for a sphere is  where
where  is the location of the sphere's center and
is the location of the sphere's center and  is the sphere's radius.
is the sphere's radius.
It is already known that the sphere's center is  . The sphere's radius is the distance between (1,2,0) and (3,4,5) which is
. The sphere's radius is the distance between (1,2,0) and (3,4,5) which is  .
.
Therefore the sphere's equation is:  .
. The general equation for a sphere is  where
where  is the location of the sphere's center and
is the location of the sphere's center and  is the sphere's radius.
is the sphere's radius.
It is already known that the sphere's center is  . The sphere's radius is the distance between (1,2,0) and (3,4,5) which is
. The sphere's radius is the distance between (1,2,0) and (3,4,5) which is  .
.
Therefore the sphere's equation is:  .
. 61. Sketch the plane passing through the points (2,0,0), (0,3,0), and (0,0,4)
62. Find the value of

if

and



 .
.
Therefore:  .
.



 .
.
Therefore:  .
.

63. Find all unit vectors parallel to

The length of  is
is  . Therefore
. Therefore  is a unit vector that points in the same direction as
is a unit vector that points in the same direction as  , and
, and  is a unit vector that points in the opposite direction as
is a unit vector that points in the opposite direction as  .
.
 are the unit vectors that are parallel to
are the unit vectors that are parallel to  .
. The length of  is
is  . Therefore
. Therefore  is a unit vector that points in the same direction as
is a unit vector that points in the same direction as  , and
, and  is a unit vector that points in the opposite direction as
is a unit vector that points in the opposite direction as  .
.
 are the unit vectors that are parallel to
are the unit vectors that are parallel to  .
. 64. Prove one of the distributive properties for vectors in

:







 .
.






 .
. 65. Find all unit vectors orthogonal to

in

66. Find all unit vectors orthogonal to

in

All vectors  that are orthogonal to
that are orthogonal to  must satisfy
must satisfy 

 .
.
The set of possible values of  is
is  . The restriction that
. The restriction that  becomes
becomes 


 .
.
The set of possible  and
and  is an ellipse with radii
is an ellipse with radii  and
and  . One possible parameterization of
. One possible parameterization of  and
and  is
is  and
and  where
where  . This parameterization yields
. This parameterization yields  where
where  as the complete set of unit vectors that are orthogonal to
as the complete set of unit vectors that are orthogonal to  .
.
Re-parameterizing by letting  gives the set
gives the set ![{\displaystyle \left\langle {\frac {4}{5}}c,-{\frac {3}{5}}c,\pm {\sqrt {1-c^{2}}}\right\rangle ,\ c\in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087456257f4b52c3bf13601c2a02680a406617d4)
All vectors  that are orthogonal to
that are orthogonal to  must satisfy
must satisfy 

 .
.
The set of possible values of  is
is  . The restriction that
. The restriction that  becomes
becomes 


 .
.
The set of possible  and
and  is an ellipse with radii
is an ellipse with radii  and
and  . One possible parameterization of
. One possible parameterization of  and
and  is
is  and
and  where
where  . This parameterization yields
. This parameterization yields  where
where  as the complete set of unit vectors that are orthogonal to
as the complete set of unit vectors that are orthogonal to  .
.
Re-parameterizing by letting  gives the set
gives the set ![{\displaystyle \left\langle {\frac {4}{5}}c,-{\frac {3}{5}}c,\pm {\sqrt {1-c^{2}}}\right\rangle ,\ c\in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087456257f4b52c3bf13601c2a02680a406617d4)
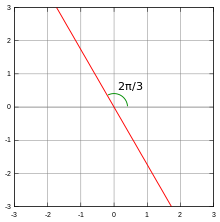
67. Find all unit vectors that make an angle of

with the vector

The angle that  makes with the x-axis is
makes with the x-axis is  counterclockwise.
counterclockwise.
Making a both a clockwise and a counterclockwise rotation of  gives
gives 





The angle that  makes with the x-axis is
makes with the x-axis is  counterclockwise.
counterclockwise.
Making a both a clockwise and a counterclockwise rotation of  gives
gives 





Find  and
and 
80.

and





81.

and





Find the area of the parallelogram with sides  and
and  .
.
82.

and

83.

and

84. Find all vectors that satisfy the equation

The cross product is orthogonal to both multiplicand vectors.  should be orthogonal to both
should be orthogonal to both  and
and  . However,
. However,  so
so  and
and  are not orthogonal. The equation
are not orthogonal. The equation  is never true, and therefore the set of vectors
is never true, and therefore the set of vectors  that satisfy the equation is
that satisfy the equation is  "None".
"None".
The cross product is orthogonal to both multiplicand vectors.  should be orthogonal to both
should be orthogonal to both  and
and  . However,
. However,  so
so  and
and  are not orthogonal. The equation
are not orthogonal. The equation  is never true, and therefore the set of vectors
is never true, and therefore the set of vectors  that satisfy the equation is
that satisfy the equation is  "None".
"None". 85. Find the volume of the parallelepiped with edges given by position vectors

,

, and

The volume of a parallelepiped with edges defined by the vectors  ,
,  , and
, and  is the absolute value of the scalar triple product:
is the absolute value of the scalar triple product:  .
.




The volume of a parallelepiped with edges defined by the vectors  ,
,  , and
, and  is the absolute value of the scalar triple product:
is the absolute value of the scalar triple product:  .
.




86. A wrench has a pivot at the origin and extends along the
x-axis. Find the magnitude and the direction of the torque at the pivot when the force

is applied to the wrench
n units away from the origin.
The moment arm is  , so the torque applied is
, so the torque applied is  The magnitude of the torque is
The magnitude of the torque is  . The torque's direction is
. The torque's direction is  .
. The moment arm is  , so the torque applied is
, so the torque applied is  The magnitude of the torque is
The magnitude of the torque is  . The torque's direction is
. The torque's direction is  .
. Prove the following identities or show them false by giving a counterexample.
Calculus of Vector-Valued Functions[edit | edit source]
100. Differentiate

.


101. Find a tangent vector for the curve

at the point

.
 so a possible a tangent vector at
so a possible a tangent vector at  is
is 
 so a possible a tangent vector at
so a possible a tangent vector at  is
is 
102. Find the unit tangent vector for the curve

.

 so the unit tangent vector is
so the unit tangent vector is 

 so the unit tangent vector is
so the unit tangent vector is 
103. Find the unit tangent vector for the curve
![{\displaystyle \mathbf {r} (t)=\langle \sin(t),\cos(t),e^{-t}\rangle ,\ t\in [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2f30552af99a8f55083220a2960a8a6697bad79)
at the point

.

 so the unit tangent vector is
so the unit tangent vector is 
At  :
: 

 so the unit tangent vector is
so the unit tangent vector is 
At  :
: 
104. Find

if

and

.
For an arbitrary  the position
the position  can be computed by the integral
can be computed by the integral  .
.





For an arbitrary  the position
the position  can be computed by the integral
can be computed by the integral  .
.





105. Evaluate









120. Find velocity, speed, and acceleration of an object if the position is given by

.
 ,
,  ,
, 
 ,
,  ,
, 
121. Find the velocity and the position vectors for

if the acceleration is given by

.




















Find the length of the following curves.
140.
![{\displaystyle \mathbf {r} (t)=\langle 4\cos(3t),4\sin(3t)\rangle ,\ t\in [0,2\pi /3].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3681f0d46ab5bdb85098ee74c0058797105aace)
For an infinitesimal step  , the length traversed is approximately
, the length traversed is approximately
 .
.
The total length is therefore:

For an infinitesimal step  , the length traversed is approximately
, the length traversed is approximately
 .
.
The total length is therefore:

141.
![{\displaystyle \mathbf {r} (t)=\langle 2+3t,1-4t,3t-4\rangle ,\ t\in [1,6].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1513778e4cae9f336be929232f7054e2840ec58f)
For an infinitesimal step  , the length traversed is approximately
, the length traversed is approximately
 .
.
The total length is therefore:

For an infinitesimal step  , the length traversed is approximately
, the length traversed is approximately
 .
.
The total length is therefore:

Parametrization and Normal Vectors[edit | edit source]
142. Find a description of the curve that uses arc length as a parameter:
![{\displaystyle \mathbf {r} (t)=\langle t^{2},2t^{2},4t^{2}\rangle \ t\in [1,4].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9715ec537d31fdc34e2ac352df9235bfa517bc28)
For an infinitesimal step  , the length traversed is approximately
, the length traversed is approximately 
Given an upper bound of ![{\displaystyle u\in [1,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7028583c2cfbfdb6d3bb92e76ba9947380b3a42f) , the arc length swept out from
, the arc length swept out from  to
to  is:
is:

The arc length spans a range from  to
to  . For an arc length of
. For an arc length of ![{\displaystyle s\in [0,15{\sqrt {21}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb5dd87fcf26f064f70ae02ce3f02e751082141e) , the upper bound on
, the upper bound on  that generates an arc length of
that generates an arc length of  is
is  , and the point at which this upper bound occurs is:
, and the point at which this upper bound occurs is: 
For an infinitesimal step  , the length traversed is approximately
, the length traversed is approximately 
Given an upper bound of ![{\displaystyle u\in [1,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7028583c2cfbfdb6d3bb92e76ba9947380b3a42f) , the arc length swept out from
, the arc length swept out from  to
to  is:
is:

The arc length spans a range from  to
to  . For an arc length of
. For an arc length of ![{\displaystyle s\in [0,15{\sqrt {21}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb5dd87fcf26f064f70ae02ce3f02e751082141e) , the upper bound on
, the upper bound on  that generates an arc length of
that generates an arc length of  is
is  , and the point at which this upper bound occurs is:
, and the point at which this upper bound occurs is: 
143. Find the unit tangent vector
T and the principal unit normal vector
N for the curve

Check that
T⋅
N=0.
A tangent vector is  . Normalizing this vector to get the unit tangent vector gives:
. Normalizing this vector to get the unit tangent vector gives:

A vector that has the direction of the principal unit normal vector is




Normalizing  gives the principal unit normal vector:
gives the principal unit normal vector:




A tangent vector is  . Normalizing this vector to get the unit tangent vector gives:
. Normalizing this vector to get the unit tangent vector gives:

A vector that has the direction of the principal unit normal vector is




Normalizing  gives the principal unit normal vector:
gives the principal unit normal vector:




Equations of Lines And Planes[edit | edit source]
160. Find an equation of a plane passing through points

Let  denote a plane that contains points
denote a plane that contains points  ,
,  , and
, and  . Let
. Let  denote an arbitrary vector that is orthogonal to
denote an arbitrary vector that is orthogonal to  , and
, and  denote the position vector of an arbitrary point contained by
denote the position vector of an arbitrary point contained by  . A point at position vector
. A point at position vector  is contained by
is contained by  if and only if the displacement from
if and only if the displacement from  is orthogonal to
is orthogonal to  . This yields the equation
. This yields the equation 
 .
.
The displacement from  to
to  , which is
, which is  , and the displacement from
, and the displacement from  to
to  , which is
, which is  , are both contained by
, are both contained by  so the cross product of these two displacements forms a candidate
so the cross product of these two displacements forms a candidate  :
: 


Any of  ,
,  , and
, and  is a candidate
is a candidate  . Let
. Let 
The equation becomes 



Let  denote a plane that contains points
denote a plane that contains points  ,
,  , and
, and  . Let
. Let  denote an arbitrary vector that is orthogonal to
denote an arbitrary vector that is orthogonal to  , and
, and  denote the position vector of an arbitrary point contained by
denote the position vector of an arbitrary point contained by  . A point at position vector
. A point at position vector  is contained by
is contained by  if and only if the displacement from
if and only if the displacement from  is orthogonal to
is orthogonal to  . This yields the equation
. This yields the equation 
 .
.
The displacement from  to
to  , which is
, which is  , and the displacement from
, and the displacement from  to
to  , which is
, which is  , are both contained by
, are both contained by  so the cross product of these two displacements forms a candidate
so the cross product of these two displacements forms a candidate  :
: 


Any of  ,
,  , and
, and  is a candidate
is a candidate  . Let
. Let 
The equation becomes 



161. Find an equation of a plane parallel to the plane 2x−y+z=1 passing through the point (0,2,-2)
Let  denote a plane that is parallel to the plane
denote a plane that is parallel to the plane  and contains the point
and contains the point  . Let
. Let  denote an arbitrary vector that is orthogonal to
denote an arbitrary vector that is orthogonal to  , and
, and  denote the position vector of an arbitrary point contained by
denote the position vector of an arbitrary point contained by  . A point at position vector
. A point at position vector  is contained by
is contained by  if and only if the displacement from
if and only if the displacement from  is orthogonal to
is orthogonal to  . This yields the equation
. This yields the equation 
 .
.
Any vector  that is orthogonal to
that is orthogonal to  is also orthogonal to
is also orthogonal to  and vice versa. Since
and vice versa. Since 
 , the coefficient vector
, the coefficient vector  is orthogonal to
is orthogonal to  , so a candidate
, so a candidate  is
is  .
.
Since point  is contained by
is contained by  , let
, let  .
.
The equation becomes 


Let  denote a plane that is parallel to the plane
denote a plane that is parallel to the plane  and contains the point
and contains the point  . Let
. Let  denote an arbitrary vector that is orthogonal to
denote an arbitrary vector that is orthogonal to  , and
, and  denote the position vector of an arbitrary point contained by
denote the position vector of an arbitrary point contained by  . A point at position vector
. A point at position vector  is contained by
is contained by  if and only if the displacement from
if and only if the displacement from  is orthogonal to
is orthogonal to  . This yields the equation
. This yields the equation 
 .
.
Any vector  that is orthogonal to
that is orthogonal to  is also orthogonal to
is also orthogonal to  and vice versa. Since
and vice versa. Since 
 , the coefficient vector
, the coefficient vector  is orthogonal to
is orthogonal to  , so a candidate
, so a candidate  is
is  .
.
Since point  is contained by
is contained by  , let
, let  .
.
The equation becomes 


162. Find an equation of the line perpendicular to the plane x+y+2z=4 passing through the point (5,5,5).
Let  denote an arbitrary plane. Let
denote an arbitrary plane. Let  denote an arbitrary vector that is orthogonal to
denote an arbitrary vector that is orthogonal to  , and
, and  denote the position vector of an arbitrary point contained by
denote the position vector of an arbitrary point contained by  . A point at position vector
. A point at position vector  is contained by
is contained by  if and only if the displacement from
if and only if the displacement from  is orthogonal to
is orthogonal to  . This yields the equation
. This yields the equation 
 . Therefore the equation that defines
. Therefore the equation that defines  is
is  .
.
The equation  is equivalent to
is equivalent to  . This implies that the coefficient vector
. This implies that the coefficient vector  is orthogonal to the plane defined by
is orthogonal to the plane defined by  . A line that passes through point
. A line that passes through point  and is parallel to
and is parallel to  is parameterized by:
is parameterized by:

Let  denote an arbitrary plane. Let
denote an arbitrary plane. Let  denote an arbitrary vector that is orthogonal to
denote an arbitrary vector that is orthogonal to  , and
, and  denote the position vector of an arbitrary point contained by
denote the position vector of an arbitrary point contained by  . A point at position vector
. A point at position vector  is contained by
is contained by  if and only if the displacement from
if and only if the displacement from  is orthogonal to
is orthogonal to  . This yields the equation
. This yields the equation 
 . Therefore the equation that defines
. Therefore the equation that defines  is
is  .
.
The equation  is equivalent to
is equivalent to  . This implies that the coefficient vector
. This implies that the coefficient vector  is orthogonal to the plane defined by
is orthogonal to the plane defined by  . A line that passes through point
. A line that passes through point  and is parallel to
and is parallel to  is parameterized by:
is parameterized by:

163. Find an equation of the line where planes x+2y−z=1 and x+y+z=1 intersect.
164. Find the angle between the planes x+2y−z=1 and x+y+z=1.
Let  denote an arbitrary plane. Let
denote an arbitrary plane. Let  denote an arbitrary vector that is orthogonal to
denote an arbitrary vector that is orthogonal to  , and
, and  denote the position vector of an arbitrary point contained by
denote the position vector of an arbitrary point contained by  . A point at position vector
. A point at position vector  is contained by
is contained by  if and only if the displacement from
if and only if the displacement from  is orthogonal to
is orthogonal to  . This yields the equation
. This yields the equation 
 . Therefore the equation that defines
. Therefore the equation that defines  is
is  .
.
Let  be the plane described by
be the plane described by  and
and  be the plane described by
be the plane described by 
Since  , the coefficient vector
, the coefficient vector  is orthogonal to
is orthogonal to  .
.
Since  , the coefficient vector
, the coefficient vector  is orthogonal to
is orthogonal to  .
.
The angle  between
between  and
and  is equivalent to the angle between
is equivalent to the angle between  and
and  :
:




Let  denote an arbitrary plane. Let
denote an arbitrary plane. Let  denote an arbitrary vector that is orthogonal to
denote an arbitrary vector that is orthogonal to  , and
, and  denote the position vector of an arbitrary point contained by
denote the position vector of an arbitrary point contained by  . A point at position vector
. A point at position vector  is contained by
is contained by  if and only if the displacement from
if and only if the displacement from  is orthogonal to
is orthogonal to  . This yields the equation
. This yields the equation 
 . Therefore the equation that defines
. Therefore the equation that defines  is
is  .
.
Let  be the plane described by
be the plane described by  and
and  be the plane described by
be the plane described by 
Since  , the coefficient vector
, the coefficient vector  is orthogonal to
is orthogonal to  .
.
Since  , the coefficient vector
, the coefficient vector  is orthogonal to
is orthogonal to  .
.
The angle  between
between  and
and  is equivalent to the angle between
is equivalent to the angle between  and
and  :
:




165. Find the distance from the point (3,4,5) to the plane x+y+z=1.
Given a unit length vector  , consider an axis
, consider an axis  oriented in the direction of
oriented in the direction of  . The "
. The " coordinate" is determined by orthogonally projecting points onto the
coordinate" is determined by orthogonally projecting points onto the  axis. Given a position vector
axis. Given a position vector  , the expression
, the expression  computes the
computes the  coordinate.
coordinate.
The equation  is equivalent to
is equivalent to



Letting  , the plane
, the plane  consists of all points whose
consists of all points whose  coordinate is
coordinate is  . The
. The  coordinate of
coordinate of  is
is  .
.
The distance between the plane  and the point
and the point  along the
along the  axis is
axis is


The distance  is the distance between the point and plane along a direction that is orthogonal to the plane, and is hence the shortest distance.
is the distance between the point and plane along a direction that is orthogonal to the plane, and is hence the shortest distance. Given a unit length vector  , consider an axis
, consider an axis  oriented in the direction of
oriented in the direction of  . The "
. The " coordinate" is determined by orthogonally projecting points onto the
coordinate" is determined by orthogonally projecting points onto the  axis. Given a position vector
axis. Given a position vector  , the expression
, the expression  computes the
computes the  coordinate.
coordinate.
The equation  is equivalent to
is equivalent to



Letting  , the plane
, the plane  consists of all points whose
consists of all points whose  coordinate is
coordinate is  . The
. The  coordinate of
coordinate of  is
is  .
.
The distance between the plane  and the point
and the point  along the
along the  axis is
axis is


The distance  is the distance between the point and plane along a direction that is orthogonal to the plane, and is hence the shortest distance.
is the distance between the point and plane along a direction that is orthogonal to the plane, and is hence the shortest distance. Evaluate the following limits.
180.







181.







At what points is the function f continuous?
183.

All points (x,y) except for (0,0) and the line y=x+1
All points (x,y) except for (0,0) and the line y=x+1
Use the two-path test to show that the following limits do not exist. (A path does not have to be a straight line.)
184.

The limit is 1 along the line y=x, and −1 along the line y=−x
The limit is 1 along the line y=x, and −1 along the line y=−x
186.

The limit is 1 along the line y=0, and −1 along the line x=0
The limit is 1 along the line y=0, and −1 along the line x=0
200. Find

if

201. Find all three partial derivatives of the function



Find the four second partial derivatives of the following functions.
202.

203.

Find 
220.

221.

222.

Find 
223.

224.

225. The volume of a pyramid with a square base is

, where
x is the side of the square base and
h is the height of the pyramid. Suppose that

and

for

Find

Find an equation of a plane tangent to the given surface at the given point(s).
240.

Start with a point  that is on the surface. Perturbing the
that is on the surface. Perturbing the  ,
,  , and
, and  coordinates by infinitesimal amounts
coordinates by infinitesimal amounts  ,
,  , and
, and  respectively, changes the value of
respectively, changes the value of  by the infinitesimal amount
by the infinitesimal amount  , and the value of
, and the value of  by
by  . To remain in the surface it must be the case that
. To remain in the surface it must be the case that 
 .
.
To linearly extrapolate the condition  to a tangent plane at
to a tangent plane at  , replace the infinitesimal perturbations
, replace the infinitesimal perturbations  ,
,  , and
, and  with large perturbations
with large perturbations  ,
,  , and
, and  to get
to get  . Any point in the tangent plane at
. Any point in the tangent plane at  can be reached by an appropriate choice of
can be reached by an appropriate choice of  ,
,  , and
, and  where
where  . Any point
. Any point  in the tangent plane at
in the tangent plane at  must satisfy
must satisfy  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is  .
.
The tangent planes are therefore:

Start with a point  that is on the surface. Perturbing the
that is on the surface. Perturbing the  ,
,  , and
, and  coordinates by infinitesimal amounts
coordinates by infinitesimal amounts  ,
,  , and
, and  respectively, changes the value of
respectively, changes the value of  by the infinitesimal amount
by the infinitesimal amount  , and the value of
, and the value of  by
by  . To remain in the surface it must be the case that
. To remain in the surface it must be the case that 
 .
.
To linearly extrapolate the condition  to a tangent plane at
to a tangent plane at  , replace the infinitesimal perturbations
, replace the infinitesimal perturbations  ,
,  , and
, and  with large perturbations
with large perturbations  ,
,  , and
, and  to get
to get  . Any point in the tangent plane at
. Any point in the tangent plane at  can be reached by an appropriate choice of
can be reached by an appropriate choice of  ,
,  , and
, and  where
where  . Any point
. Any point  in the tangent plane at
in the tangent plane at  must satisfy
must satisfy  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is  .
.
The tangent planes are therefore:

241.

Start with a point  that is on the surface. Perturbing the
that is on the surface. Perturbing the  ,
,  , and
, and  coordinates by infinitesimal amounts
coordinates by infinitesimal amounts  ,
,  , and
, and  respectively, changes the value of
respectively, changes the value of  by the infinitesimal amount
by the infinitesimal amount  , and the value of
, and the value of  by
by 


 . To remain in the surface it must be the case that
. To remain in the surface it must be the case that 
 .
.
To linearly extrapolate the condition  to a tangent plane at
to a tangent plane at  , replace the infinitesimal perturbations
, replace the infinitesimal perturbations  ,
,  , and
, and  with large perturbations
with large perturbations  ,
,  , and
, and  to get
to get  . Any point in the tangent plane at
. Any point in the tangent plane at  can be reached by an appropriate choice of
can be reached by an appropriate choice of  ,
,  , and
, and  where
where  . Any point
. Any point  in the tangent plane at
in the tangent plane at  must satisfy
must satisfy  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is  .
.
The tangent planes are therefore:

Start with a point  that is on the surface. Perturbing the
that is on the surface. Perturbing the  ,
,  , and
, and  coordinates by infinitesimal amounts
coordinates by infinitesimal amounts  ,
,  , and
, and  respectively, changes the value of
respectively, changes the value of  by the infinitesimal amount
by the infinitesimal amount  , and the value of
, and the value of  by
by 


 . To remain in the surface it must be the case that
. To remain in the surface it must be the case that 
 .
.
To linearly extrapolate the condition  to a tangent plane at
to a tangent plane at  , replace the infinitesimal perturbations
, replace the infinitesimal perturbations  ,
,  , and
, and  with large perturbations
with large perturbations  ,
,  , and
, and  to get
to get  . Any point in the tangent plane at
. Any point in the tangent plane at  can be reached by an appropriate choice of
can be reached by an appropriate choice of  ,
,  , and
, and  where
where  . Any point
. Any point  in the tangent plane at
in the tangent plane at  must satisfy
must satisfy  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is  .
.
The tangent planes are therefore:

242.

Start with a point  that is on the surface. Perturbing the
that is on the surface. Perturbing the  ,
,  , and
, and  coordinates by infinitesimal amounts
coordinates by infinitesimal amounts  ,
,  , and
, and  respectively, changes the value of
respectively, changes the value of  by the infinitesimal amount
by the infinitesimal amount  , and the value of
, and the value of  by
by  . To remain in the surface it must be the case that
. To remain in the surface it must be the case that 
 .
.
To linearly extrapolate the condition  to a tangent plane at
to a tangent plane at  , replace the infinitesimal perturbations
, replace the infinitesimal perturbations  ,
,  , and
, and  with large perturbations
with large perturbations  ,
,  , and
, and  to get
to get  . Any point in the tangent plane at
. Any point in the tangent plane at  can be reached by an appropriate choice of
can be reached by an appropriate choice of  ,
,  , and
, and  where
where  . Any point
. Any point  in the tangent plane at
in the tangent plane at  must satisfy
must satisfy  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is 

Start with a point  that is on the surface. Perturbing the
that is on the surface. Perturbing the  ,
,  , and
, and  coordinates by infinitesimal amounts
coordinates by infinitesimal amounts  ,
,  , and
, and  respectively, changes the value of
respectively, changes the value of  by the infinitesimal amount
by the infinitesimal amount  , and the value of
, and the value of  by
by  . To remain in the surface it must be the case that
. To remain in the surface it must be the case that 
 .
.
To linearly extrapolate the condition  to a tangent plane at
to a tangent plane at  , replace the infinitesimal perturbations
, replace the infinitesimal perturbations  ,
,  , and
, and  with large perturbations
with large perturbations  ,
,  , and
, and  to get
to get  . Any point in the tangent plane at
. Any point in the tangent plane at  can be reached by an appropriate choice of
can be reached by an appropriate choice of  ,
,  , and
, and  where
where  . Any point
. Any point  in the tangent plane at
in the tangent plane at  must satisfy
must satisfy  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is 

243.

Start with a point  that is on the surface. Perturbing the
that is on the surface. Perturbing the  ,
,  , and
, and  coordinates by infinitesimal amounts
coordinates by infinitesimal amounts  ,
,  , and
, and  respectively, changes the value of
respectively, changes the value of  by the infinitesimal amount
by the infinitesimal amount  , and the value of
, and the value of  by
by  . To remain in the surface it must be the case that
. To remain in the surface it must be the case that 
 .
.
To linearly extrapolate the condition  to a tangent plane at
to a tangent plane at  , replace the infinitesimal perturbations
, replace the infinitesimal perturbations  ,
,  , and
, and  with large perturbations
with large perturbations  ,
,  , and
, and  to get
to get  . Any point in the tangent plane at
. Any point in the tangent plane at  can be reached by an appropriate choice of
can be reached by an appropriate choice of  ,
,  , and
, and  where
where  . Any point
. Any point  in the tangent plane at
in the tangent plane at  must satisfy
must satisfy  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is 


Start with a point  that is on the surface. Perturbing the
that is on the surface. Perturbing the  ,
,  , and
, and  coordinates by infinitesimal amounts
coordinates by infinitesimal amounts  ,
,  , and
, and  respectively, changes the value of
respectively, changes the value of  by the infinitesimal amount
by the infinitesimal amount  , and the value of
, and the value of  by
by  . To remain in the surface it must be the case that
. To remain in the surface it must be the case that 
 .
.
To linearly extrapolate the condition  to a tangent plane at
to a tangent plane at  , replace the infinitesimal perturbations
, replace the infinitesimal perturbations  ,
,  , and
, and  with large perturbations
with large perturbations  ,
,  , and
, and  to get
to get  . Any point in the tangent plane at
. Any point in the tangent plane at  can be reached by an appropriate choice of
can be reached by an appropriate choice of  ,
,  , and
, and  where
where  . Any point
. Any point  in the tangent plane at
in the tangent plane at  must satisfy
must satisfy  .
.
The point  lies in the surface, and the tangent plane is
lies in the surface, and the tangent plane is 


Maximum And Minimum Problems[edit | edit source]
Find critical points of the function f. When possible, determine whether each critical point corresponds to a local maximum, a local minimum, or a saddle point.
How to find local minimums, local maximums, and saddle points for a function with an unconstrained domain.
Start with a candidate point  , and envision that the
, and envision that the  and
and  coordinates are changing at rates of
coordinates are changing at rates of  and
and  respectively:
respectively:  and
and  . The rate of change in
. The rate of change in  is
is

 .
.
 is a local minimum only if
is a local minimum only if  for all
for all  . This occurs iff
. This occurs iff  .
. is a local maximum only if
is a local maximum only if  for all
for all  . This occurs iff
. This occurs iff  .
.
Points where  are "critical points" and may contain a local minimum, a local maximum, or a saddle point. It is then needed to classify the critical point.
are "critical points" and may contain a local minimum, a local maximum, or a saddle point. It is then needed to classify the critical point.
The second derivative is


 .
.
- A critical point is a local minimum iff
 for all
for all  .
.
- A critical point is a local maximum iff
 for all
for all  .
.
- A critical point that is neither a local minimum nor a local maximum is a saddle point.
While it will not be shown here,  can attain both positive and negative values iff
can attain both positive and negative values iff  .
.
- A critical point is a local minimum if
 and
and 
- A critical point is a local maximum if
 and
and 
- A critical point is a saddle point if

The quantity  will be called the "discriminant".
will be called the "discriminant".
260.

The first order derivatives are:  and
and  . Finding the critical points is done by solving the equations
. Finding the critical points is done by solving the equations 
 . Substituting
. Substituting  in place of
in place of  in the first equation gives
in the first equation gives  . This gives the critical points
. This gives the critical points  .
.
The second order derivatives are  ;
;  ; and
; and  . The discriminant is:
. The discriminant is:  .
.
For critical point  , the discriminant is
, the discriminant is  and
and  so
so  is a local minimum.
is a local minimum.
For critical point  , the discriminant is
, the discriminant is  so
so  is a saddle point.
is a saddle point.
For critical point  , the discriminant is
, the discriminant is  and
and  so
so  is a local minimum.
is a local minimum.
Local minima at (1,1) and (−1,−1), saddle at (0,0) The first order derivatives are:  and
and  . Finding the critical points is done by solving the equations
. Finding the critical points is done by solving the equations 
 . Substituting
. Substituting  in place of
in place of  in the first equation gives
in the first equation gives  . This gives the critical points
. This gives the critical points  .
.
The second order derivatives are  ;
;  ; and
; and  . The discriminant is:
. The discriminant is:  .
.
For critical point  , the discriminant is
, the discriminant is  and
and  so
so  is a local minimum.
is a local minimum.
For critical point  , the discriminant is
, the discriminant is  so
so  is a saddle point.
is a saddle point.
For critical point  , the discriminant is
, the discriminant is  and
and  so
so  is a local minimum.
is a local minimum.
Local minima at (1,1) and (−1,−1), saddle at (0,0) 261.

The first order derivatives are:  and
and  . Finding the critical points is done by solving the equations
. Finding the critical points is done by solving the equations 
 and
and  . So the only critical point is
. So the only critical point is  .
.
The second order derivatives are  ;
;  ; and
; and  . The discriminant is
. The discriminant is 


For the critical point  , the discriminant is
, the discriminant is  so
so  is a saddle point.
is a saddle point.
Saddle at (0,0) The first order derivatives are:  and
and  . Finding the critical points is done by solving the equations
. Finding the critical points is done by solving the equations 
 and
and  . So the only critical point is
. So the only critical point is  .
.
The second order derivatives are  ;
;  ; and
; and  . The discriminant is
. The discriminant is 


For the critical point  , the discriminant is
, the discriminant is  so
so  is a saddle point.
is a saddle point.
Saddle at (0,0) 262.

The first order derivatives are:  and
and  . Finding the critical points is done by solving the equations
. Finding the critical points is done by solving the equations 

 . The critical points are
. The critical points are  .
.
The second order derivatives are:  ;
;  ; and
; and  . The discriminant is
. The discriminant is 
 .
.
For critical point  , the discriminant is
, the discriminant is  so
so  is a saddle point.
is a saddle point.
For critical points  and
and  , the discriminant is
, the discriminant is  and
and  so
so  and
and  are local maximums.
are local maximums.
For critical points  and
and  , the discriminant is
, the discriminant is  and
and  so
so  and
and  are local minimums.
are local minimums.
Saddle at (0,0), local maxima at  local minima at
local minima at 
The first order derivatives are:  and
and  . Finding the critical points is done by solving the equations
. Finding the critical points is done by solving the equations 

 . The critical points are
. The critical points are  .
.
The second order derivatives are:  ;
;  ; and
; and  . The discriminant is
. The discriminant is 
 .
.
For critical point  , the discriminant is
, the discriminant is  so
so  is a saddle point.
is a saddle point.
For critical points  and
and  , the discriminant is
, the discriminant is  and
and  so
so  and
and  are local maximums.
are local maximums.
For critical points  and
and  , the discriminant is
, the discriminant is  and
and  so
so  and
and  are local minimums.
are local minimums.
Saddle at (0,0), local maxima at  local minima at
local minima at 
Find absolute maximum and minimum values of the function f on the set R.
How to find candidate points for the absolute minimum and maximum of a function with a constrained domain.
Let  denote the function for which the absolute minimum and maximum is sought. Let the domain be constrained to all points
denote the function for which the absolute minimum and maximum is sought. Let the domain be constrained to all points  where
where  where
where  is an appropriate function over
is an appropriate function over  .
.
Start with a candidate point  where
where  , and envision that the
, and envision that the  and
and  coordinates are changing at rates of
coordinates are changing at rates of  and
and  respectively:
respectively:  and
and  . The rate of change in
. The rate of change in  is
is

 . Since it is required that
. Since it is required that  , it must be the case that
, it must be the case that 
 .
.
 is a local minimum or maximum only if
is a local minimum or maximum only if  for all
for all  where
where  . This occurs iff the gradient
. This occurs iff the gradient  is parallel to the gradient
is parallel to the gradient  . This condition can be quantified by
. This condition can be quantified by  where factor
where factor  is a "Lagrange multiplier".
is a "Lagrange multiplier".
Points  where
where  and
and  for some
for some  are candidate points for the absolute minimum or maximum. If the domain has any corners, then these corners are also candidate points.
are candidate points for the absolute minimum or maximum. If the domain has any corners, then these corners are also candidate points.
263.

Candidate points will be derived from two sources: Critical points of the function  assuming an unconstrained domain, and candidate points assuming the restriction
assuming an unconstrained domain, and candidate points assuming the restriction  .
.
The first order derivatives of  are
are  and
and  , so the only critical point where
, so the only critical point where  occurs at
occurs at  . This critical point lies in
. This critical point lies in  so it remains a valid candidate.
so it remains a valid candidate.  .
.
The first order derivatives of  are
are  and
and  . Candidate points assuming the restriction
. Candidate points assuming the restriction  must satisfy
must satisfy  for some
for some  . These equations are equivalent to
. These equations are equivalent to  . If
. If  , then the only restriction left on
, then the only restriction left on  is
is  and
and  . This gives two candidate points
. This gives two candidate points  . If
. If  , then
, then  which is never true. Hence the only valid candidate points derived by restricting the domain to
which is never true. Hence the only valid candidate points derived by restricting the domain to  are
are  .
.  and
and  .
.
In total, the candidates are  ,
,  , and
, and  .
.
The absolute minimum of  occurs at
occurs at  , and the absolute maximum of
, and the absolute maximum of  occurs at
occurs at  .
.
Maximum of 9 at (0,−2) and minimum of 0 at (0,1) Candidate points will be derived from two sources: Critical points of the function  assuming an unconstrained domain, and candidate points assuming the restriction
assuming an unconstrained domain, and candidate points assuming the restriction  .
.
The first order derivatives of  are
are  and
and  , so the only critical point where
, so the only critical point where  occurs at
occurs at  . This critical point lies in
. This critical point lies in  so it remains a valid candidate.
so it remains a valid candidate.  .
.
The first order derivatives of  are
are  and
and  . Candidate points assuming the restriction
. Candidate points assuming the restriction  must satisfy
must satisfy  for some
for some  . These equations are equivalent to
. These equations are equivalent to  . If
. If  , then the only restriction left on
, then the only restriction left on  is
is  and
and  . This gives two candidate points
. This gives two candidate points  . If
. If  , then
, then  which is never true. Hence the only valid candidate points derived by restricting the domain to
which is never true. Hence the only valid candidate points derived by restricting the domain to  are
are  .
.  and
and  .
.
In total, the candidates are  ,
,  , and
, and  .
.
The absolute minimum of  occurs at
occurs at  , and the absolute maximum of
, and the absolute maximum of  occurs at
occurs at  .
.
Maximum of 9 at (0,−2) and minimum of 0 at (0,1) 264.
 R
R is a closed triangle with vertices (0,0), (2,0), and (0,2).
Triangle  is defined by the constraints
is defined by the constraints  ,
,  , and
, and  .
.
Candidate points for the absolute minimum and maximum will be derived from 5 sources:
- Critical points of the function
 assuming an unconstrained domain.
assuming an unconstrained domain.
- Candidate points assuming the restriction
 .
.
- Candidate points assuming the restriction
 .
.
- Candidate points assuming the restriction
 .
.
- The vertex points
 .
.
The first order derivatives of  are
are  and
and  , so the only critical point where
, so the only critical point where  is
is  . The critical point
. The critical point  lies in
lies in  so it remains a valid candidate.
so it remains a valid candidate.  .
.
The first order derivatives of  are
are  and
and  . Candidate points assuming the restriction
. Candidate points assuming the restriction  must satisfy
must satisfy  for some
for some  . These equations are equivalent to
. These equations are equivalent to  . This yields the candidate point
. This yields the candidate point  . Point
. Point  lies in
lies in  so it remains a valid candidate.
so it remains a valid candidate.  .
.
The first order derivatives of  are
are  and
and  . Candidate points assuming the restriction
. Candidate points assuming the restriction  must satisfy
must satisfy  for some
for some  . These equations are equivalent to
. These equations are equivalent to  . This yields the candidate point
. This yields the candidate point  . Point
. Point  lies in
lies in  so it remains a valid candidate.
so it remains a valid candidate.  .
.
The first order derivatives of  are
are  and
and  . Candidate points assuming the restriction
. Candidate points assuming the restriction  must satisfy
must satisfy  for some
for some  . The second equation yields
. The second equation yields  . Substituting
. Substituting  in place of
in place of  in the third equation gives
in the third equation gives  . Substituting
. Substituting  in place of
in place of  in the first equation gives
in the first equation gives  , which then yields
, which then yields  and
and  . This yields the candidate point
. This yields the candidate point  . Point
. Point  lies in
lies in  so it remains a valid candidate.
so it remains a valid candidate.  .
.
Finally, we add the vertices  to the lineup of candidate points.
to the lineup of candidate points.
Evaluating  at each candidate point gives
at each candidate point gives  ;
;  ;
;  ;
;  ;
;  ; and
; and  . The absolute minimum of
. The absolute minimum of  occurs at
occurs at  , while the absolute maximum of
, while the absolute maximum of  occurs at all of
occurs at all of  .
.
Maximum of 0 at (2,0), (0,2), and (0,0); minimum of −2 at (1,1) Triangle  is defined by the constraints
is defined by the constraints  ,
,  , and
, and  .
.
Candidate points for the absolute minimum and maximum will be derived from 5 sources:
- Critical points of the function
 assuming an unconstrained domain.
assuming an unconstrained domain.
- Candidate points assuming the restriction
 .
.
- Candidate points assuming the restriction
 .
.
- Candidate points assuming the restriction
 .
.
- The vertex points
 .
.
The first order derivatives of  are
are  and
and  , so the only critical point where
, so the only critical point where  is
is  . The critical point
. The critical point  lies in
lies in  so it remains a valid candidate.
so it remains a valid candidate.  .
.
The first order derivatives of  are
are  and
and  . Candidate points assuming the restriction
. Candidate points assuming the restriction  must satisfy
must satisfy  for some
for some  . These equations are equivalent to
. These equations are equivalent to  . This yields the candidate point
. This yields the candidate point  . Point
. Point  lies in
lies in  so it remains a valid candidate.
so it remains a valid candidate.  .
.
The first order derivatives of  are
are  and
and  . Candidate points assuming the restriction
. Candidate points assuming the restriction  must satisfy
must satisfy  for some
for some  . These equations are equivalent to
. These equations are equivalent to  . This yields the candidate point
. This yields the candidate point  . Point
. Point  lies in
lies in  so it remains a valid candidate.
so it remains a valid candidate.  .
.
The first order derivatives of  are
are  and
and  . Candidate points assuming the restriction
. Candidate points assuming the restriction  must satisfy
must satisfy  for some
for some  . The second equation yields
. The second equation yields  . Substituting
. Substituting  in place of
in place of  in the third equation gives
in the third equation gives  . Substituting
. Substituting  in place of
in place of  in the first equation gives
in the first equation gives  , which then yields
, which then yields  and
and  . This yields the candidate point
. This yields the candidate point  . Point
. Point  lies in
lies in  so it remains a valid candidate.
so it remains a valid candidate.  .
.
Finally, we add the vertices  to the lineup of candidate points.
to the lineup of candidate points.
Evaluating  at each candidate point gives
at each candidate point gives  ;
;  ;
;  ;
;  ;
;  ; and
; and  . The absolute minimum of
. The absolute minimum of  occurs at
occurs at  , while the absolute maximum of
, while the absolute maximum of  occurs at all of
occurs at all of  .
.
Maximum of 0 at (2,0), (0,2), and (0,0); minimum of −2 at (1,1)
Finding the locations and shortest distances between two surfaces.
Consider two surfaces  and
and  in 3D space defined by the equations
in 3D space defined by the equations  and
and  respectively. Given a point
respectively. Given a point  from
from  and a point
and a point  from
from  , if
, if  and
and  are the points that minimize the distance between
are the points that minimize the distance between  and
and  , then it must be the case that the displacement
, then it must be the case that the displacement  is perpendicular to both surfaces. The gradient vector
is perpendicular to both surfaces. The gradient vector  is orthogonal to
is orthogonal to  , and the gradient vector
, and the gradient vector  is orthogonal to
is orthogonal to  . The displacement vector must be parallel to both gradient vectors:
. The displacement vector must be parallel to both gradient vectors:  for some
for some  and
and  .
.
Candidate points for the shortest distance between two surfaces must satisfy the following 8 equations:  for some
for some  and
and  .
.
265. Find the point on the plane x−y+z=2 closest to the point (1,1,1).
The plane is defined by the equation  , and a normal vector to the plane is
, and a normal vector to the plane is  . The closest point
. The closest point  on the plane to the point
on the plane to the point  is the point where the displacement
is the point where the displacement  is parallel to
is parallel to  . The following equations must be satisfied:
. The following equations must be satisfied:  .
.
The second equation gives  , and replacing
, and replacing  with
with  in the third and forth equations gives
in the third and forth equations gives  and
and  respectively. In the first equation, replacing
respectively. In the first equation, replacing  with
with  and
and  with
with  gives
gives  . This gives in turn
. This gives in turn  and
and  .
.
The only candidate point for the closest distance is  , so therefore the point on the plane
, so therefore the point on the plane  that is closest to the point
that is closest to the point  is
is  .
. The plane is defined by the equation  , and a normal vector to the plane is
, and a normal vector to the plane is  . The closest point
. The closest point  on the plane to the point
on the plane to the point  is the point where the displacement
is the point where the displacement  is parallel to
is parallel to  . The following equations must be satisfied:
. The following equations must be satisfied:  .
.
The second equation gives  , and replacing
, and replacing  with
with  in the third and forth equations gives
in the third and forth equations gives  and
and  respectively. In the first equation, replacing
respectively. In the first equation, replacing  with
with  and
and  with
with  gives
gives  . This gives in turn
. This gives in turn  and
and  .
.
The only candidate point for the closest distance is  , so therefore the point on the plane
, so therefore the point on the plane  that is closest to the point
that is closest to the point  is
is  .
. 266. Find the point on the surface

closest to the plane

The surface is defined by the equation  , and the plane is defined by the equation
, and the plane is defined by the equation  . Given a point
. Given a point  from the surface and a point
from the surface and a point  from the plane, these two points are closest to each other only if (but not always if) the displacement vector
from the plane, these two points are closest to each other only if (but not always if) the displacement vector  is a parallel to the surface normal vector
is a parallel to the surface normal vector  and the plane normal vector
and the plane normal vector  . There must exist factors
. There must exist factors  and
and  such that the following 8 equations hold:
such that the following 8 equations hold: 
The fifth equation is equivalent to  , and the eighth equation is equivalent to
, and the eighth equation is equivalent to  . Eliminating via substitution
. Eliminating via substitution  and
and  in all of the other equations gives:
in all of the other equations gives: 
If  , then
, then  and
and  , and then
, and then  and
and  are the same point which corresponds to an intersection between the surface and the plane. While it will not be shown here, it is relatively simple to show that the surface and plane fail to intersect. Excluding the possibility that
are the same point which corresponds to an intersection between the surface and the plane. While it will not be shown here, it is relatively simple to show that the surface and plane fail to intersect. Excluding the possibility that  , the equations
, the equations  and
and  together imply that
together imply that  ; and the equations
; and the equations  and
and  together imply that
together imply that  . The values
. The values  and
and  give
give  . Hence the point on the surface
. Hence the point on the surface  that is closest to the plane
that is closest to the plane  is
is  .
.
From  and
and  , it follows that
, it follows that  and
and  . In the equation
. In the equation  , eliminating
, eliminating  and
and  via substitution gives
via substitution gives  . Hence
. Hence  and
and  . The corresponding closest point on the plane is
. The corresponding closest point on the plane is  .
.
The closest point on the surface is  .
. The surface is defined by the equation  , and the plane is defined by the equation
, and the plane is defined by the equation  . Given a point
. Given a point  from the surface and a point
from the surface and a point  from the plane, these two points are closest to each other only if (but not always if) the displacement vector
from the plane, these two points are closest to each other only if (but not always if) the displacement vector  is a parallel to the surface normal vector
is a parallel to the surface normal vector  and the plane normal vector
and the plane normal vector  . There must exist factors
. There must exist factors  and
and  such that the following 8 equations hold:
such that the following 8 equations hold: 
The fifth equation is equivalent to  , and the eighth equation is equivalent to
, and the eighth equation is equivalent to  . Eliminating via substitution
. Eliminating via substitution  and
and  in all of the other equations gives:
in all of the other equations gives: 
If  , then
, then  and
and  , and then
, and then  and
and  are the same point which corresponds to an intersection between the surface and the plane. While it will not be shown here, it is relatively simple to show that the surface and plane fail to intersect. Excluding the possibility that
are the same point which corresponds to an intersection between the surface and the plane. While it will not be shown here, it is relatively simple to show that the surface and plane fail to intersect. Excluding the possibility that  , the equations
, the equations  and
and  together imply that
together imply that  ; and the equations
; and the equations  and
and  together imply that
together imply that  . The values
. The values  and
and  give
give  . Hence the point on the surface
. Hence the point on the surface  that is closest to the plane
that is closest to the plane  is
is  .
.
From  and
and  , it follows that
, it follows that  and
and  . In the equation
. In the equation  , eliminating
, eliminating  and
and  via substitution gives
via substitution gives  . Hence
. Hence  and
and  . The corresponding closest point on the plane is
. The corresponding closest point on the plane is  .
.
The closest point on the surface is  .
. Double Integrals over Rectangular Regions[edit | edit source]
Evaluate the given integral over the region R.
280.
![{\displaystyle \displaystyle \iint _{R}(x^{2}+xy)dA,\ R=\{(x,y)\mid x\in [1,2],\ y\in [-1,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed365e6e7ddc55551e813614af01d9c10cdc9af6)


281.
![{\displaystyle \displaystyle \iint _{R}(xy\sin(x^{2}))dA,\ R=\{(x,y)\mid x\in [0,{\sqrt {\pi /2}}],\ y\in [0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d8c966096be3b39bffd752544bc134cb87182)


282.
![{\displaystyle \displaystyle \iint _{R}{\frac {x}{(1+xy)^{2}}}dA,\ R=\{(x,y)\mid x\in [0,4],\ y\in [1,2]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1d6288e4ccdb0134f6d2546fdd60591316f57ca)


Evaluate the given iterated integrals.
Double Integrals over General Regions[edit | edit source]
Evaluate the following integrals.
300.
 R
R is bounded by
x=0,
y=2
x+1, and
y=5−2
x.


301.
 R
R is in the first quadrant and bounded by
x=0,

and



Use double integrals to compute the volume of the given region.
Double Integrals in Polar Coordinates[edit | edit source]
323. Evaluate

if
R is the unit disk centered at the origin.


In the following exercises, sketching the region of integration may be helpful.
341. Find the volume of the solid in the first octant bounded by the plane 2x+3y+6z=12 and the coordinate planes.


342. Find the volume of the solid in the first octant bounded by the cylinder

for
![{\displaystyle y\in [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0281fdf747a9247ed8a56221ddd07b34c2a50097)
, and the planes
y=
x and
x=0.


344. Rewrite the integral

in the order
dydzdx.


Cylindrical And Spherical Coordinates[edit | edit source]
361. Find the mass of the solid cylinder
![{\displaystyle D=\{(r,\theta ,z)\mid r\in [0,3],\ z\in [0,2]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3d5655e4f2397642509c6640400d7087e95cf35)
given the density function



362. Use a triple integral to find the volume of the region bounded by the plane
z=0 and the hyperboloid



363. If
D is a unit ball, use a triple integral in spherical coordinates to evaluate



364. Find the mass of a solid cone
![{\displaystyle \{(\rho ,\phi ,\theta )\mid \phi \leq \pi /3,\ z\in [0,4]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f200079667c56d8b47444f8062308745eb385015)
if the density function is



Center of Mass and Centroid[edit | edit source]
380. Find the center of mass for three particles located in space at (1,2,3), (0,0,1), and (1,1,0), with masses 2, 1, and 1 respectively.


384. Find the centroid of the region in the first quadrant bounded by

,

, and

.


385. Find the center of mass for the region
![{\displaystyle \{(x,y)\mid x\in [0,4],y\in [0,2]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e476dabc9b7a7dfe36cd98372488912496465f7)
, with the density



386. Find the center of mass for the triangular plate with vertices (0,0), (0,4), and (4,0), with density



One can sketch two-dimensional vector fields by plotting vector values, flow curves, and/or equipotential curves.
402. Find and sketch the gradient field

for the potential function

for

and

.


403. Find the gradient field

for the potential function



420. Evaluate

if
C is the line segment from (0,0) to (5,5)


421. Evaluate

if
C is the circle of radius 4 centered at the origin


422. Evaluate

if
C is the helix
![{\displaystyle \mathbf {r} (t)=\langle 3\cos(t),3\sin(t),t\rangle ,\ t\in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c08e2103ca08229383eb122b8d4d0b8dba3eac9)


423. Evaluate

if

and
C is the arc of the parabola
![{\displaystyle \mathbf {r} (t)=\langle 4t,t^{2}\rangle ,\ t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/642cd051fef71427b9ff15e0885d8b70e1d1f344)


Conservative Vector Fields[edit | edit source]
Determine if the following vector fields are conservative on 
440.

441.

Determine if the following vector fields are conservative on their respective domains in  When possible, find the potential function.
When possible, find the potential function.
442.



443.



460. Evaluate the circulation of the field

over the boundary of the region above
y=0 and below
y=
x(2-
x) in two different ways, and compare the answers.


461. Evaluate the circulation of the field

over the unit circle centered at the origin in two different ways, and compare the answers.


462. Evaluate the flux of the field

over the square with vertices (0,0), (1,0), (1,1), and (0,1) in two different ways, and compare the answers.


482. Find the curl of



484. Prove that the general rotation field

, where

is a non-zero constant vector and

, has zero divergence, and the curl of

is

.
If  , then
, then
 , and then
, and then


If  , then
, then
 , and then
, and then


500. Give a parametric description of the plane



501. Give a parametric description of the hyperboloid

![{\displaystyle \langle {\sqrt {v^{2}-1}}\cos(u),{\sqrt {v^{2}-1}}\sin(u),v\rangle ,\ u\in [0,2\pi ],\ |v|\geq 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e30ae2582ed79c8841a5ec44ce9a38adb627be5)
![{\displaystyle \langle {\sqrt {v^{2}-1}}\cos(u),{\sqrt {v^{2}-1}}\sin(u),v\rangle ,\ u\in [0,2\pi ],\ |v|\geq 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e30ae2582ed79c8841a5ec44ce9a38adb627be5)
502. Integrate

over the portion of the plane
z=2−
x−
y in the first octant.


504. Find the flux of the field

across the surface of the cone
![{\displaystyle z^{2}=x^{2}+y^{2},\ z\in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdef9c8592f3f4001cfc49e3df0f914ece0b10df)
with normal vectors pointing in the positive
z direction.


505. Find the flux of the field

across the surface
![{\displaystyle y=x^{2},\ z\in [0,4],\ x\in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75190cd1fce58f3ae022e60f9e482de598e957cd)
with normal vectors pointing in the positive
y direction.


520. Use a surface integral to evaluate the circulation of the field

on the boundary of the plane

in the first octant.


522. Use a line integral to find

where

,

is the upper half of the ellipsoid

, and

points in the direction of the
z-axis.


523. Use a line integral to find

where

,

is the part of the sphere

for

, and

points in the direction of the
z-axis.


Compute the net outward flux of the given field across the given surface.
540.

,

is a sphere of radius

centered at the origin.


542.

,

is the boundary of the cube



543.

,

is the surface of the region bounded by the paraboloid

and the
xy-plane.


544.

,

is the boundary of the region between the concentric spheres of radii 2 and 4, centered at the origin.


545.

,

is the boundary of the region between the cylinders

and

and cut off by planes

and




























































































![{\displaystyle \left[-{\frac {\pi }{6}},+{\frac {\pi }{6}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c1c4ad280f407a250a7e9003e81c427970c4863)





































































![{\displaystyle \left\langle {\frac {4}{5}}c,-{\frac {3}{5}}c,\pm {\sqrt {1-c^{2}}}\right\rangle ,\ c\in [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087456257f4b52c3bf13601c2a02680a406617d4)






































































![{\displaystyle \mathbf {r} (t)=\langle \sin(t),\cos(t),e^{-t}\rangle ,\ t\in [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2f30552af99a8f55083220a2960a8a6697bad79)




































![{\displaystyle \mathbf {r} (t)=\langle 4\cos(3t),4\sin(3t)\rangle ,\ t\in [0,2\pi /3].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3681f0d46ab5bdb85098ee74c0058797105aace)



![{\displaystyle \mathbf {r} (t)=\langle 2+3t,1-4t,3t-4\rangle ,\ t\in [1,6].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1513778e4cae9f336be929232f7054e2840ec58f)


![{\displaystyle \mathbf {r} (t)=\langle t^{2},2t^{2},4t^{2}\rangle \ t\in [1,4].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9715ec537d31fdc34e2ac352df9235bfa517bc28)

![{\displaystyle u\in [1,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7028583c2cfbfdb6d3bb92e76ba9947380b3a42f)




![{\displaystyle s\in [0,15{\sqrt {21}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb5dd87fcf26f064f70ae02ce3f02e751082141e)





























































































































































































































































































































































































































































































![{\displaystyle \displaystyle \iint _{R}(x^{2}+xy)dA,\ R=\{(x,y)\mid x\in [1,2],\ y\in [-1,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed365e6e7ddc55551e813614af01d9c10cdc9af6)

![{\displaystyle \displaystyle \iint _{R}(xy\sin(x^{2}))dA,\ R=\{(x,y)\mid x\in [0,{\sqrt {\pi /2}}],\ y\in [0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d8c966096be3b39bffd752544bc134cb87182)

![{\displaystyle \displaystyle \iint _{R}{\frac {x}{(1+xy)^{2}}}dA,\ R=\{(x,y)\mid x\in [0,4],\ y\in [1,2]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1d6288e4ccdb0134f6d2546fdd60591316f57ca)














![{\displaystyle R=\{(x,y)\mid y\in [0,1],\ x\in [y,1]\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/856d2cf8e1925376bee04c19cab0d5776798d7e3)





![{\displaystyle R=\{(r,\theta )\mid r\in [1,3],\ \theta \in [0,\pi /2]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd2b79af3799bfeb6786939cced1210962a85ae2)


![{\displaystyle \{(r,\theta )\mid r\in [2,4]\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f34d27bc87605d3269e518c127c478a3854701e)








![{\displaystyle y\in [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0281fdf747a9247ed8a56221ddd07b34c2a50097)







![{\displaystyle D=\{(r,\theta ,z)\mid r\in [0,3],\ z\in [0,2]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3d5655e4f2397642509c6640400d7087e95cf35)






![{\displaystyle \{(\rho ,\phi ,\theta )\mid \phi \leq \pi /3,\ z\in [0,4]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f200079667c56d8b47444f8062308745eb385015)






![{\displaystyle x\in [0,\pi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6060e8cfe67c32952064ce30d10d000735967451)

![{\displaystyle x\in [0,4].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/246b2cdb5a7eb4ef2a89385af8652d13e75c1afb)







![{\displaystyle \{(x,y)\mid x\in [0,4],y\in [0,2]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e476dabc9b7a7dfe36cd98372488912496465f7)

















![{\displaystyle \mathbf {r} (t)=\langle 3\cos(t),3\sin(t),t\rangle ,\ t\in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c08e2103ca08229383eb122b8d4d0b8dba3eac9)



![{\displaystyle \mathbf {r} (t)=\langle 4t,t^{2}\rangle ,\ t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/642cd051fef71427b9ff15e0885d8b70e1d1f344)


































![{\displaystyle \langle {\sqrt {v^{2}-1}}\cos(u),{\sqrt {v^{2}-1}}\sin(u),v\rangle ,\ u\in [0,2\pi ],\ |v|\geq 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e30ae2582ed79c8841a5ec44ce9a38adb627be5)



![{\displaystyle z=x^{2}+y^{2},\ z\in [0,4].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41908c387a7d4b76f5e34372862a7379b14c0707)


![{\displaystyle z^{2}=x^{2}+y^{2},\ z\in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdef9c8592f3f4001cfc49e3df0f914ece0b10df)

![{\displaystyle y=x^{2},\ z\in [0,4],\ x\in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75190cd1fce58f3ae022e60f9e482de598e957cd)































