Basic Physics of Nuclear Medicine/Sonography & Nuclear Medicine

This is a developing chapter of a wikibook entitled Basic Physics of Nuclear Medicine.
Sonography is an application of the SONAR principle in medical imaging where the surfaces of internal organs and their inner structure can be depicted (see the image below). This imaging modality has the advantage of not using ionizing radiation and is frequently used to provide correlative anatomical information for nuclear medicine images. An overview of basic features of sonographic imaging is provided in this chapter.
We'll start with a consideration of relevant characteristics of sound waves before describing various imaging methods.
Sound Waves[edit | edit source]
Sound waves travelling through air consist of periodic fluctuations in air pressure, called compressions and rarefactions, as illustrated below:

These longitudinal waves travel with a velocity, v, of about 330 m/s in air at STP, and at higher velocities in denser media, such as water and soft tissue. Indeed a medium is needed for the waves to propagate – remember that the physics behind the statement 'In space no one can hear you scream', which was used to promote the movie Alien, is quite correct!
A sequence of compressions and rarefactions is referred to as one cycle, as illustrated. The wavelength, λ, is defined as the length of one cycle and the frequency, f, as the number of cycles which pass a fixed point every second. These quantities are related through the famous equation:
The human ear is sensitive to sound frequencies up to about 20 kHz, and waves of higher frequency are referred to as ultrasound. Much higher frequencies are used in diagnostic sonography, in the range 1-15 MHz. Low frequencies in this range can be used to image large deep structures, while high frequencies can be used for small, superficial objects.
| Medium | Velocity (m/s) |
|---|---|
| Air | 331 |
| Brain | 1,541 |
| Kidney | 1,561 |
| Liver | 1,549 |
| Muscle | 1,585 |
| Fat | 1,450 |
| Soft Tissue (average) | 1,540 |
The velocity of ultrasound waves is identical to that of sound waves in the same medium, and is given in the following table for a range of internal organs. Note that a velocity of 1,540 m/s is generally assumed for soft tissue in sonographic imaging and represents an average of that for a number of tissues, muscles and organs.
Ultrasound waves are generally produced in pulses for sonographic imaging, with the time interval between pulses used to detect ultrasound echoes produced within the body. This technique exploits what's known as the Pulse-Echo Principle, as illustrated in the diagram below. The upper half of the diagram depicts an ultrasound transducer emitting one pulse of ultrasound into a hypothetical body, which is assumed to consist of just two tissues. The lower half of the diagram depicts the situation after the ultrasound pulse has encountered the interface between the two tissues. A reflected pulse is shown travelling back towards the transducer, i.e. the echo, and a transmitted pulse is seen to continue into the second tissue.
The length of time taken for the pulse, once produced by the transducer, to travel to the interface and the echoed pulse to return is termed the pulse-echo time, t, and its measurement allows the depth, d, of the interface to be determined using the following equation:
Note that in this equation:
- the average velocity of ultrasound in the tissue is used, and
- the factor, 2, arises because the pulse and its echo must travel the same distance, one from the transducer to the interface and the other from the interface back to the transducer:

Ultrasound transducers exploit the piezoelectric effect to cause a crystal to vibrate at ultrasound frequencies. The resultant vibrations generate pulses of compressions and rarefactions which propagate through the tissues. Echoes produced by tissue interfaces are then detected by the same crystal – exploiting the piezoelectric effect once again.
The ultrasound pulse becomes attenuated as it passes through tissue and four phenomena result when it encounters a tissue interface, as illustrated below:
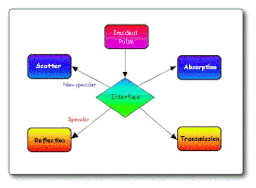
| Interface | Reflection Coefficient (%) |
|---|---|
| Soft Tissue – Air | 99.9 |
| Fat – Muscle | 1.08 |
| Fat – Kidney | 0.64 |
| Muscle – Liver | 1.5 |
Some of the energy in the pulse is scattered through a process called non-specular reflection, some of it generates an echo in a specular reflection process, some of it is transmitted through the interface to produce further echoes at other interfaces and a small amount is absorbed. The reflectivity of an interface depends on the acoustic impedance of the two tissues involved, and representative values are shown in the table.
Notice in the table that a huge reflection can occur at a soft tissue – air interface. Its for this reason that a coupling medium is used between the transducer and the patient's skin. Internal reflections are seen in the table to be of the order of 1%, yielding a useful transparency for imaging purposes.
Ultrasound Scanner[edit | edit source]
A simplified block diagram of a sonography system is shown in the figure below. The type of scanner shown operates using a linear array transducer, which we'll learn more about shortly. We can see the Master Timer in the top right of the figure. This circuit sets the number of ultrasound pulses which the transducer generates every second – a factor referred to as the Pulse Repetition Frequency (PRF). Its also seen that echo pulses picked up by the transducer are amplified by a Receiver Amplifier whose output is demodulated before being fed to a Scan Converter so that the location and amplitude of detected echoes can be displayed.

The Time-Gain Compensation (TGC) circuit provides for selective amplification of the echo signals so as to compensate for attenuation of distant ultrasound echoes and suppress more proximal ones. The switch array is used to excite the multiple crystals in the transducer as shown below:


In the simplest arrangement, each crystal generates an ultrasound pulse one after the other so that sequential lines of tissue can be rapidly and continuously insonated.
The ultrasound image is referred to as a B-Mode scan and consists of a 2D representation of the echo pattern in a cross-section of tissue with the transducer position at the top of the image. The locations of echo-producing tissue interfaces are generally represented by bright pixels on a dark background, with the amplitude of each echo signal being represented by the pixel value – see the image on the right.
The image shown was actually acquired using a more sophisticated transducer called a phased array, which generates a sector-shaped scan. This type of transducer also uses a linear array of small crystals, but with them excited in complex timing sequences, controlled by delay circuitry – as shown in the figure below. The ultrasound beam can be steered to scan a region in this manner while being focussed at different depths simultaneously.

There are numerous other transducer designs, each of which have particular advantages in different clinical applications. Two designs of mechanical transducer are shown below as examples. The left panel illustrates a transducer with a single crystal which is rocked back and forth during the scanning process, while the right panel illustrates a rotating arrangement of single crystals:

Components of the scan conversion circuitry are illustrated in the following figure:

The figure illustrates the process of digitizing the analogue echo signals using an analogue-to-digital converter (ADC) and applying pre-processing to the digital data using an input look-up table (ILUT) prior to storage in random access memory. This memory is filled in the sequence which was used to scan the patient and read out in a manner suitable for the display device, which is typically an LCD monitor. Prior to display, the image data can be post-processed using an output look-up table (OLUT) so that contrast enhancement and other processing functions can be applied. Note that we've encountered this type of digital image processing in a more general form in another chapter of this wikibook. The box labelled μP represents a microprocessor which is used to control this scan conversion circuitry, as well as many other functions of the scanner, e.g. the timing used for phased array emission and reception.
A digital image resolution widely used in sonography is 512 x 512 x 8-bits – a magnified view of the central region of the liver scan shown earlier is provided below to illustrate the digital nature of the data:

We conclude this section with photos of a sonography system and typical transducers:

Doppler Ultrasound[edit | edit source]
The Doppler Effect is widely exploited in the remote measurement of moving objects, and can be used in medical sonography to generate images (and sounds!) of flowing blood. The effect is demonstrated by all wave-like phenomena, be they longitudinal or transverse waves, and has been used with light, for instance, to reveal that we live in an expanding universe! Its also exploited using radio waves in highway speed traps, and can be experienced with sound waves when an ambulance passes by with its siren blaring.
Let's take the example of a train engine sounding its whistle, as illustrated in the diagram below:

When the train is stationary, and there isn't a wind blowing, the sound will emanate equally from the whistle in all directions, as illustrated on the left. When the train is moving, however, sound frequencies will be increased in the forward direction and reduced in the opposite direction, as illustrated on the right, to an extent dependent on the velocity of the train. This apparent change in frequency of the sound waves experienced by a stationary listener is referred to as the Doppler Shift.
The situation for exploiting the Doppler Effect for the detection of blood flow is illustrated in the following diagram:

The diagram shows a Doppler transducer placed on the skin and aimed at an angle, θ, towards a blood vessel, which contains blood flowing with a velocity of u m/s, at any instant. The transducer emits ultrasound waves of frequency, fo, and echoes generated by moving reflectors in the blood, e.g. red blood cells, have a frequency, fr. The difference between these two frequencies, Δf, is related to the velocity of the flowing reflectors through the following equation:
where v is the velocity of sound in the medium.
So, for instance, when ultrasound with a frequency in the range 2-10 MHz is applied in medicine to detect blood flowing in arteries (where typical velocities are 0-5 m/s), the equation above reveals that the frequency differences will be in the audible range of sound frequencies, i.e. 0-15 kHz. Their signals can therefore be fed through speakers so that this sound can be heard.
Its also possible to examine the frequency content of Doppler shifts to examine subtle details of the distribution of blood velocities during a cardiac cycle by computing their Fourier transforms. Its more common however to produce images of the distribution of frequency shifts within blood vessels using techniques such as Colour-Flow or Colour-Power imaging. These techniques are used to automatically fuse Doppler signals with B-Mode ultrasound images, as illustrated below:

Colour-flow processing is sensitive to the direction of blood flow, i.e. it can detect both positive and negative Doppler shifts, and uses a colour look-up table (CLUT) so that shifts in one direction are displayed in shades of red with those in the other direction in shades of blue – as illustrated by a patient's jugular vein and carotid artery depicted in the left panel of the figure above. A simplified block diagram of a sonography system used for such imaging is shown below:

The system uses a beam former circuit to excite the crystals of the phased array transducer for B-Mode imaging and Doppler shift detection in a rapid alternating manner, with the echo signals being fed to B-Mode scanning circuitry and the Doppler signals fed to an autocorrelation detector for analysis. Output data from these circuits are then blended within the scan conversion and formatting circuitry, prior to display of the fused image.
As a final point, note that the colour-power image displayed above does not contain any blood-flow direction information, since this technique computes the power of reflected Doppler-shifted pulses instead of their frequency content.

