Analogue Electronics/BJTs/Active Mode
Active Mode[edit | edit source]
In the Emitter[edit | edit source]
Recall from the previous page that a BJT in active mode has its emitter-base junction in forward bias and its collector-base junction (CBJ) in reverse. This means, for an NPN device, that the emitter is at a lower potential than the base, which is lower than the collector. Generally, the voltage between the collector and base is larger than the voltage between the emitter and base.

The EBJ is forward biased, so electrons will be injected from the emitter into the base. Also, some holes will be injected into the emitter from the base, but the emitter is much more heavily doped than the base, so this current is small (this is the preferable situation, so transistors are designed and made like this).
The electrons flowing out of the emitter and the holes flowing in together constitute the emitter current, iE, which is defined to be "out of" the emitter lead. As we said before, this current is dominated by the electron flow.
We might expect the electrons to be either "stuck" in the base, or to be removed via the base, as the CBJ is reverse biased, and therefore we do not expect it to be conducting. However, recall that when a pn junction is reverse biased like this, all that it means is that holes cannot travel from left to right, and electrons cannot go from right to left. Normally, this results in no current, as there are no electrons present in p-type material.
In the Base[edit | edit source]
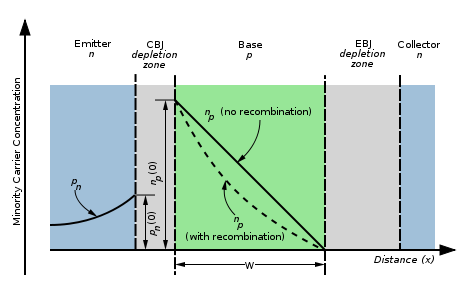
Let us now look at what happens to the electrons injected into the base. Because the base is made of p-type silicon, the electrons are minority carriers. The base is very thin (the diagram above is not to scale), so the electron concentration, np, will have a linear characteristic. This is explained in Semiconductors, and we will not try to prove it here. The electron concentration will be highest at the emitter side of the base, and will be zero at the collector side. It is zero here because the CBJ is in reverse bias, causing all minority carriers to be attracted to and swept across to the collector (by the same token, majority carriers, holes, are repelled from the junction). We will term the electron concentration at the EBJ np(0).
The EBJ is in forward bias, so the concentration at the emitter side of the base np(0) will be proportional to evBE/vT:
[Electron Concentration at EBJ side of Base]
where
- np0 is the thermal equilibrium concentration of electrons in the base
- vBE is the forward voltage across the EBJ
- VT is the thermal voltage (about 25 mV at room temperature - 300K)
The decreasing concentration of electrons in the base as we move toward the collector causes a diffusion current in this direction (electrons try to diffuse to lower concentrations). This diffusion current, In is proportional to the gradient of the electron concentration:
[Electron current in the Base]
where
- x is the distance of a point from the EBJ
- AE is the cross sectional area of the EBJ
- q is the magnitude charge on an electron (a positive quantity)
- Dn is the electron diffusivity in the base
- W is the effective width of the base (taking into account reduction due to depletion zones)
For more information on exactly why this is, see Semiconductors.
Due to the negative slope of the electron concentration, we get a negative current (with respect to x), which means that it flows right-left. This is not surprising, as electrons are negatively charged, so a diffusion form left to right leads to a current from right to left.
Because the electrons here are in a p-type material populated with holes, some will recombine with the holes in the base. Due to the base being very thin, this is a small proportion of the total number of electrons. This effect causes the electron concentration in the base to be slightly non linear (dashed line in the above diagram). Because the concentration is higher near the EBJ, we expect a larger number of electrons to recombine per unit length than we do at the CBJ, so the line is steeper at the EBJ, leading the "dished" shape shown in the diagram.
In summary so far, we are injecting electrons into the base from the emitter, and these are readily swept up by the electric field across the CBJ. The base is made very thin to allow just this to occur. A small number of electrons will recombine with the holes (which are the majority carriers) in the base layer. However, the base is very thin, so the electrons are usually swept up before they can recombine. This means that a large current will flow through the transistor from emitter to base. A smaller current, made up of the holes flowing into the emitter and the recombining holes makes up the base current.
This is why the emitter and collector are so named - the emitter emits electrons into the base, and the collector collects them from the base.
Collector Current[edit | edit source]
In the sections above, we saw that the majority of the electrons diffusing across the base make it to the CBJ, whereupon they are swept up by the electric field across the CBJ, which is in reverse bias. These "swept-up" electrons constitute the collector current, iC Therefore, we can say that:
- .
Since In is negative, this implies that the collector current is negative too, with respect to our direction of increasing x. This means a current from right to left, so flowing into the collector lead. In the equations below, we will remove the negative sign, and work with the magnitude of the current.
Thus:
Substituting for np(0) from above, we get:
We now define a quantity called the saturation current as follows:
- ,
leading to:
[Collector Current]
- .
We can also substitute np0=ni2/NA into our expression for IS:
[Saturation Current]
Note here that the collector current does not depend on the voltage across the CBJ, vCB. So long as the CBJ is in reverse bias, the electrons that reach the CBJ will be removed into the collector.
Our newly defined saturation current, 'IS is inversely proportional to the width of the base, W, and directly proportional to the area of the EBJ. The saturation current can generally be expected to lie in the range of 10−18 to 10−12 A. It is very much affected by temperature as it proportional to the square intrinsic electron concentration. Therefore, it is also proportional to the cube of the absolute temperature. This is explained in Semiconductors. For an actual transistor, the saturation current will be given by the manufacturer on the datasheet.
As the saturation current is related to the ratio of the EBJ area and the width of the base, it is also known as the scale current. This is a frequently-used principle in the field of IC design, as two transistors that are identical except for EBJ area will have, for the same vBE, collector currents differing by a factor equal to the ratio of the EBJ areas.
Base Current[edit | edit source]
We have already seen that there are two components to the base current: the holes injected into the emitter (iB1) and the holes that are supplied (via diffusion) to replace those lost by recombination with electrons in transit from emitter to collector. This is iB2.
iB1 is given by the equation for a forward-biased pn-junction, similar to that used earlier:
where:
- AE is the cross sectional area of the EBJ
- Lp is the hole diffusion length
- Dp is the hole diffusivity in the base
- ND is the doping concentration of the emitter
Note that because the emitter is very long (as opposed to the very short base), we do not use the emitter length, but rather Lp, the diffusion length of the holes.
iB2 can be evaluated by looking at the average time that it takes for an electron in the base to recombine. This time, called the minority-carrier lifetime, is denoted by τb. In this case, in this time, all the electrons in the base (constituting a charge Qn) will have recombined.
In a steady state, this charge will be constantly replenished by the electrons flowing in from the emitter. in order for the electrons to be replenished to maintain a steady state, the injected current must supply the base with a (positive) charge of:
[Base Recombination Current related to Minority-Carrier Lifetime]
The minority carrier charge stored in the base in steady-state is related to the area under the triangle formed by the electron-concentration curve (which is a straight line), which can be seen in the diagram above. Multiplying by the volume of the base, electronic charge and the maximum concentration, np(0), we get the total charge to be:
Substituting for np(0) and then for np0 gives:
Substituting from the equation relating iB2 to τb, we get:
Now, the total base current is given by:
This unwieldy form can be simplified somewhat by applying the expression for the saturation current and factoring out the exponential part:
As an aside here, notice that the part given by iB1 is related to the following ratios:
- Hole to electron diffusivity
- Acceptor to donor doping concentration
- Base width the hole diffusion length in the emitter
We now define a quantity called β as follows:
β is a scalar quantity (see here for confirmation) that is defined entirely by the physical properties of the transistor. We can see that it relates the base and collector current:
- .
β generally takes a value of between 50 and 300 for "normal" transistors, but for more expensive devices (especially those sold in IC form such as the SSM2210), it can reach 1000. β is often called the common-emitter current gain. It is also often called hFE. This is due to convention in circuit theory. To see why, see this page.
We can see that β is influence by some parameter related to the production process rather than the physical properties of the semiconductor. In order to obtain high β, we can make the base width, W, very small and dope the emitter very heavily compared to the base. Also, note that so far, we have assumed that β is constant for a given transistor. We shall see soon that this is not necessarily the case, but it is frequently a useful approximation.
Emitter Current[edit | edit source]
From Kirchhoff's Current Law, we know that all current entering the transistor must also leave the transistor. Given the "default" current direction for each of the terminals of the device, we see that:
Using the relationship between iB and iC, we have
We can also define α such that:
- .
α is therefore:
We can easily see from this that α is less than, but close to, unity. Substituting with α in the expression for iE, gives
Rearranging the expression for α, we also have:
α is termed the common-base current gain. α and β describe the transistor in forward-active mode only (reverse active operation is different). Sometimes it may be necessary to explicitly show this, by writing αF and βF. These can be used interchangeably with α and β.
It is also possible to consider the action of a BJT in active mode using energy band diagrams. This explanation can be found on this page.
Large Signal Models[edit | edit source]
In the previous section, we saw how the NPN BJT behaves in the forward-active mode. That is, the base is at a higher potential than the emitter and the collector is at a higher potential than the base. We can use the properties to "convert" a BJT to simpler components for analysis. The models will work for all signals, and so are called large-signal equivalent models, or LSEMs.
The Common-Base LSEM[edit | edit source]
The forward biased EBJ causes a current to flow in the collector that is exponential with base-emitter voltage, vBE. This current is not related to the voltage of the collector, as long as it is greater than that of the base (so the CBJ is in reverse bias). The BJT thus behaves like a (non-linear) voltage-controlled current source, controlled by vBE.
The base current is a fraction, given by the emitter current divided by β, and the emitter current is the sum of the collector and base currents. Generally, β is large, so the base current is small, and emitter current is approximately equal to the collector current.
From the above description of an NPN BJT, we can derive an equivalent circuit model that describes the BJT in terms of simpler components:

Diode DE has a current of iE in it. From above, we have:
We can call the saturation current for the diode, I_{SE}. The current in the collector was previously established to be given by:
Therefore, we can see that iC is related to iE by dividing by α. We also saw this previously in the section where α was derived.
We now have a BJT model that describes all the currents in terms of vBE, and is reference to the base voltage. Let us now consider this model as a two-port network, with the input port being between the emitter and the base, and the output port between the collector and the base. The base is therefore common. As we can see, the current gain is equal to α, hence the naming of α the common-base current gain:

The Common-Emitter LSEM[edit | edit source]
We can also have a BJT model referenced to a common emitter:

The collector current is given, just as for the common-base configuration, by:
We know that the base current is given by the collector current divided by β:
We can therefore easily see that the collector current is related to the base current by:
- .
As before, we consider the current from base to emitter to flow through an internal diode. This time, we call it DB, but now its saturation current is given by:































