A Roller Coaster Ride through Relativity/Simultaneity
Simultaneity[edit | edit source]
There is a curious paradox connected with length contraction which I shall call the train in the tunnel paradox. A train whose length when at rest is agreed by all observers to be 100 m enters a tunnel whose length is also exactly 100 m. The train stops in the tunnel and everybody agrees that when the engine is flush with the exit, the guard's van is flush with the entrance.

Some time later, the train passes through the same tunnel at high speed - 80% of the velocity of light in fact. At this speed the g factor is 1.67 and to the man standing by the track at the entrance to the tunnel the train appears to be only 60 m long and spends an appreciable amount of time completely inside the tunnel.

The engine driver, however, sees things rather differently. To him it is the tunnel which is whizzing past at 80% of the velocity of light and which is in consequence shrunk to 60 m in length.

Surely they can't both be right? To put it even more forcibly, suppose the man beside the track is in fact a terrorist and his mission is to trap the train in the tunnel by blowing up the exit at the instant the back of the train enters the entrance? Will he succeed or won't he? To the engine driver, at the instant the back of the train enters the tunnel, the engine is already outside it!
In order to sort out the train in the tunnel paradox, we have to ask ourselves how the terrorist is going to arrange his devious trap. He could arrange for an optical signal, triggered by the passage of the last carriage into the tunnel, to blow up the other end of the tunnel - but light does not travel instantaneously and, by the time the signal has triggered the explosion, at least part of the train might already have emerged from the tunnel.
What he must do is send the signal in advance. We must suppose that he knows how fast the train is going and how short it is going to be, so it is easy for him to calculate the time delay needed between the instant the front of the train enters the tunnel and the time the signal needs to be sent.
Sure enough, when the time comes, the signal is sent and at the instant the back of the train enters the tunnel, the explosion at the front goes off and the whole train is wrecked.
What does the train driver think of all this? He reasons (quite correctly) that at the instant that (to him) the back of the train enters the tunnel he will be well out of the tunnel and in no danger of being trapped inside by the simultaneous explosions but, as he approaches the tunnel, he is horrified to see the terrorist (whose clock appear to be going so s-l-o-w-l-y) set off the light signal far too early. What is more, the tunnel is so short the light signal takes no time at all to get to the far end and the explosion goes off just before the engine reaches the end of the tunnel. Meanwhile, the back of the train (which to the engine driver appears not to have yet entered the tunnel) continues to move as if unaware of the carnage ahead and, at the instant the last carriage enters the tunnel, the second explosion goes off and the terrorists triumph is complete!
The truth is that events which are simultaneous to the terrorist are not simultaneous to the engine driver.
We had better take a careful look at what we mean by events being simultaneous to one observer first of all. When the terrorist says that to him the two explosions were simultaneous, he doesn't mean that he saw them happen at the same time. Since he is standing at the tunnel entrance, he sees the explosion happening at the other end (event X) after it actually happens. In fact he actually sees three distinct events from where he is standing:
- Event A: light signal sent to the front of the tunnel.
- Event B: explosion set off at the back of the tunnel.
- Event C: light returns from the explosion at the front of the tunnel.
Here is a diagram showing the terrorists point of view:

Now, according to the terrorist, event B happens exactly half way between events A and C. It is this equality which justifies his assertion that event X (the explosion at the front of the tunnel) happens at the same time as event B, the explosion at the back.
Why doesn't the driver agree with this analysis? Well, according to him, he is stationary and it is the tunnel which is moving. He sees the light pulse travelling at the speed of light towards the front of the tunnel but he also sees the front of the tunnel rushing towards the light pulse. To him, therefore, the time taken for the light pulse to get to the front of the tunnel is quite short. (This is like Beatrice on her home run.) The light takes an age to return, however, as the tunnel is now travelling in the same direction as the light beam. Of course, the driver will agree that the second explosion (the one at the back) goes off exactly half way between the sending of the signal and the arrival of the light from the first explosion but he will not agree that it is simultaneous with the first explosion. On the contrary, he will maintain that it happens much later.
To the engine driver, it seems as if space and time are no longer at right angles and the 'lines of simultaneity' are tilted forward at an angle. The signal seems to reach the front of the train quite quickly and therefore to him, the explosion at the front seems to occur before the explosion at the back.

To put it another way, since the engine driver is convinced that the explosion at the front occurs before the explosion at the back, the explosion at the front is already history when the explosion at the back happens. So events which happen at places in front of you (ie in the direction towards which you are moving) are shifted further into the past while events behind you are shifted towards the future.
Lets pursue this idea a bit further. Two observers who are stationary with respect to one another can agree about simultaneous events even if they are a long way apart. It makes perfect sense therefore to think about what is happening now on some distant star providing you are not moving with respect to that star.
Imagine that you have an alien friend who lives on the planet Mishtar in the Rigel star system. Rigel (the brightest star in the constellation Orion) is 1000 light-years away from Earth and, we shall suppose, the planet Mishtar is very like Earth and has a year exactly equal to one Earth year. One day you receive a message saying that your alien friend is this minute celebrating his 5,000 birthday (you must suppose that Mishtarians have discovered the secret of eternal life too!). It makes perfect sense to reason that since the signal has taken 1000 years to reach you, your friend is actually 6,000 years old now.
But, as you raise your glass in salutation, you suddenly realise that in the month of September, Earth is rushing towards Orion at a speed of 30 km s−1 (that is 0.0001 light years per year and so you must apply a relativistic correction to this calculation. When you move towards a distant star, your perception of what is happening now on that star changes. As we have seen, it is shifted by a certain amount into the past. The formula for the change in time on that distant star as you move towards it at a velocity v is this:
where l is the distance between you and the star as measured when you are at rest with respect to the star. (for a proof of this formula see Appendix C)
Now, working in years and light years, v = 0.0001 light-years per year, and of course c = 1 light-year per year, so ΔT = 1000 x 0.0001 = 0.1 years = 36.5 days. So just by moving towards him you can make your Mistarian friend older by 36.5 days! You are too late! You should have celebrated his birthday a month ago!
The time change may not sound much but the effect increases with distance, so time on a galaxy 1,000,000 light years away varies by as much as 100 years as the Earth swings around its orbit about the Sun. And even walking towards a galaxy 1 billion light years away changes time there by 5 years!
Of course, like time dilation and length contraction, the effect is not real. You can't actually make someone older by moving towards them. What we are saying is that when you change you speed, you also completely change your perspective of what is simultaneous.
You can explain the Twin's Paradox like this. From the point of view of your twin brother on stationary Earth, you (travelling on your state-of-the-art Astro-cruiser to Alpha Centauri at 80% of the velocity of light) simply age more slowly than he does and return 10 years later only 6 years older. From your point of view, it is he who ages more slowly and in the first 3 outward years of your journey, he will only age by 1.8 years. But when you turn round, your perception of what is now suddenly changes by DT = lv/c2 = 4 x (2 x 0.8) = 6.4 years. (The factor of 2 is because your speed changes from -0.8c to +0.8c.) When you get back, you find that your brother is 1.8 + 6.4 + 1.8 = 10 years older!
The question of what is now on a distant star is, of course, quite academic because the whole point is that you are not there to check it! but it might occur to you that if you can change the time at which events on a distant planet seem to occur just by moving around, you might be able to change the order in which events at different places occur. Well, as a matter of fact you can. If your friend on the distant star (A) happens to have a (slightly older) twin brother who lives on another star (B) 1000 light years away in the opposite direction. By moving away from star B and towards star A you can make the younger brother older than the elder brother! Or to put it another way, you can arrange it so that (to you) the younger brother's birthday happens before the elder brother's birthday!
Wait a minute you say. If you can change the order in which events occur, is it possible to make the effect precede its cause? We have met several bizarre consequences so far, could this be another one? If so, you could travel backward in time . . . You could go and kill your own grandmother . . .
No you couldn't! Relativity may be bizarre but it is not illogical! You can indeed alter the order of events, but only if they happen in different places. What is more, the events have to be fairly close together in time as well. To be more specific, you can only reverse the order of two events if a light beam triggered by event A cannot reach B before event B happens. We can summarise this as follows:
| Reassuringly normal consequence number 6 |
|---|
| Although the motion of an observer can alter the order in which some events appear to happen, relativity is entirely consistent with the laws of cause and effect. |
Mind you, this does imply one terribly important consequence which we must add to our list:
| Interesting consequence number 7 |
|---|
| It is absolutely impossible to send a signal of any sort at a speed faster than that of light in a perfect vacuum. |
Why? What would happen if you could?
Well, let us suppose that at some time in the future, your friend on Mishtar tells you the secret of instantaneous telepathy. One day you get a telepathic message from Mishtar with wonderful news. Your friend has reached the grand age of 10,000 years and he is giving a big party for all his friends right now. Of course, you respond by instantly conveying your congratulations. Nothing wrong in that – provided that you and your friend are stationary with respect to each other.
But suppose that, having received the message, you get into a spaceship and accelerate in the direction away from Orion. If moving towards a distant star makes your friend older, moving away from it will make him younger (always from your point of view, of course). If you were to accelerate to a speed of 30 km s−1, you would make him 36.5 days younger and if you sent your congratulations to him now, he would receive the reply before he had sent his initial message! If this sort of thing was possible, then, with the aid of an accomplice on a distant planet, you could effectively predict the future by telling your distant friend what has just happened and getting him to return the information several days earlier! This is nonsense!
The fact is - no signal of any sort can travel faster than the speed of light.
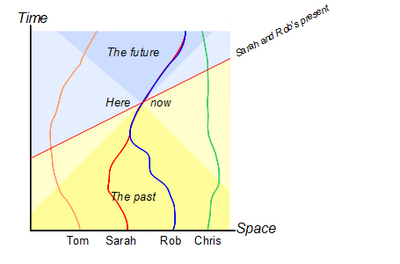
If we have to abandon the notion of simultaneity, we also have to rethink the concepts of past, present and future. Our usual picture of the nature of time can be represented something like this:.

The 'present' is a line which moves inexorably up the diagram gradually turning 'future' events (coloured blue) in to 'past' events (coloured yellow). Four characters in this simple universe are represented by 'world lines' which snake their way up the diagram. For Sarah and Rob, the point labelled 'Here/Now' appears to have special significance.
Relativity forces us to take a rather different view. Since different observers have a different perception of now, we must divide spacetime into four regions – the real past (yellow), the real future (blue) and what I shall call the inaccessible past (pale yellow) and the inaccessible future (pale blue). Real past and future are therefore contained within an hourglass shape whose limits represent the speed of light (On the diagram below the speed of light is represented by a 450 line.)

For any individual at a point in spacetime (called the here/now) the real past contains all events which could in principle have a causal effect on the here/now by a signal which travels no faster than light. The inaccessible past contains all those events which happened so recently and/or are so far away that no signal could possibly reach the here/now from them. Likewise the real future is the collection of all events which could, in principle be causally affected by a signal sent from the here/now while the inaccessible future is the collection of events which have not happened yet but which we cannot in any way influence because light does not have time to reach them.
If we consider Sarah and Rob to be at rest when they meet, their now is a horizontal line. But if they move say to the right, relativity causes their 'now' to incline upwards like this:
In fact it works rather like a pair of scissors. If the world line makes an angle of 200 with the vertical time axis, the now line makes an angle of 200 to the horizontal space axis. Note that, by moving with the right speed, any point in the inaccessible past or inaccessible future can be made simultaneous with the 'here/now'. In a sense, then, both the inaccessible past and the inaccessible future must be considered to be part of the potential present.
At the instant depicted in the diagram Sarah and Rob happen to be on a spaceship moving to the right and both Tom and Chris are stationary (ie their world lines are vertical) where their world lines intersect Sarah and Rob's 'now'. Since they are stationary, Chris' present and Tom's present are horizontal lines. Chris' present crosses Sarah and Rob's real future while Tom's present crosses their real past. These lines are shown in the next diagram.

If Sarah could have an instantaneous telepathic conversation with Chris it might go something like this:
"Hi Chris! I have just met this great guy called Rob and we are going to celebrate New Year on Mishtar.”
"Well that's great news, Sarah, and I sure hope you get along - but surely New Year on Mishtar was last week?"
Likewise, if Rob sends a telepathic message to Tom, he will be seriously puzzled because, according to him, Rob and Sarah have not yet met!
Of course, the vital thing to appreciate is that faster than light messages are forbidden. If all messages travel at the speed of light or less, there is no illogicality because all events are eventually seen to happen in the same order from all observers points of view. We do, however, have to accept that there is no such thing as 'the present'. Each observer has a now, but different observers simply have different nows.
I see. It is as if past and future have some fuzzyness where they meet
That's right. But they always come together in sharp distinction at the here/now. Some authors, have taken the blurring of past present and future to imply that the passage of time is an illusion. In fact this is an age old idea and I do not believe that Special Relativity lends any weight to it at all. Each of us has a real past and each of us has a real future. The fact that we cannot always agree on what exactly constitutes the present is just another of those bizarre consequences which we just have to accept.
| Bizarre consequence number 8 |
|---|
| Although everyone can agree on what constitutes a person's past and future, nobody can agree on what constitutes a person's present. |
The Switchback[edit | edit source]
It is quite a relief after toying with the idea that effects might precede their cause to see the world right itself and for things to look normal again as the roller coaster enters a high speed switchback. From here, you have a clear view of the rifle range. Next to it is one of those whirling roundabouts which have little model aeroplanes which fly round and round a tall pole.
That looks like fun. you say. Do you see the boys in those aeroplanes?
As we watch the boys we see that they have guns mounted in the noses of the planes and as they whirl round, they are firing at the targets on the rifle range.
Seeing those boys has given me an idea. Suppose I have a gun which can fire bullets at 80% of the speed of light and suppose I fire them from the front of my spaceship which is travelling at 80% of the speed of light. Surely the bullets will be travelling faster than light then?
Good idea, but speeds don't add up like that in relativity. In fact there is an important theorem about the addition of velocities which I shall call:
| Bizarre consequence number 9 |
|---|
| Speeds do not add up in the usual way and the result of adding two speeds together is always less than the speed of light however great the original speeds are. |
