A-level Mathematics/OCR/M1/Force as a mk Vector
| A Wikibookian suggests that this book or chapter be merged into A-level_Mathematics/OCR/M1/Force as a Vector. Please discuss whether or not this merge should happen on the discussion page. |
Vectors[edit | edit source]
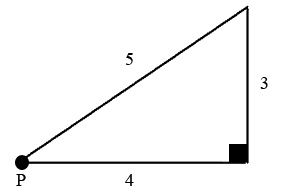
A vector is a quantity that has both a magnitude (or a size) and a direction. The opposite of vectors are scalars. Scalars only have a magnitude. There is no direction. For example, speed is a scalar as speed is the same regardless of direction. This is best illustrated as a triangle:
Our point, P, is a plane travelling along the hypotenuse of this triangle at a speed of . Its velocity, however, is not 5. As velocity is a vector and has both magnitude and direction, the speed of P is equal to moving at a velocity of along the horizontal and along the vertical.
There are several different ways of writing this as a vector. One of the most common is the i and j notation. Where i is the horizontal component of the velocity and j is the vertical component of the velocity. Using this notation, our plane would have a velocity of (4i + 3j)
Another common way of writing vectors is in the form of where x is the horizontal component and y is the vertical component. Using our plane as the example, is this vector form its velocity would be .
To change a Vector into its horizontal and vertical components we:
1. Draw a triangle representing the vector.
2. Label all known values on triangle.
3. Use trigonometry to solve.
E.g. A force, P, with magnitude 25N has a direction of (arcsin is the opposite of .), find the horizontal and vertical components of P
Triangle
Label triangle:
Use trigonometry: is is then is . Sin is O/H. Therefore the vertical component of P is 7. The Horizontal component can be found by using Pythagoras' theorem or recognising 7, 24, 25 as a Pythagorean triple. Pythagoras' theorem says that += where c is the hypotenuse and a and b are the adjacent and opposite (order does not matter). Therefore = = 576. = 24. In i and js this is (24i+7j).